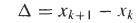Sistema híbrido de captación de energía solar-radiofrecuencia para terminales 5G de quinta generación

 Sistema híbrido de captación de energía solar-radiofrecuencia para terminales 5G de quinta generación Carlos Gordón1(B) , Danny Merino1 , Myriam Cumbajín2 , y Carlos Peñafiel3 1 Grupo de Investigación GITED, Facultad de Ingeniería en Sistemas, Electrónica e Industrial, Universidad Técnica de Ambato, UTA, 180207 Ambato, Ecuador {cd.gordon,dmerino2235}@uta.edu.ec 2 Centro de Investigación SISau, Facultad de Ingeniería, Industria y Producción, Universidad Tecnológica Indoamérica, UTI, 180103 Ambato, Ecuador myriamcumbajin@uti.edu.ec 3 Facultad de Ingeniería , Universidad Nacional de Chimborazo, UNACH, 060108 Riobamba, Ecuador carlospenafiel@unach.edu.ec

 Resumen.

 Este trabajo describe en detalle el proceso de diseño e implementación de un Sistema Híbrido de Captación de Energía Solar-Radiofrecuencia para Terminales 5G de Quinta Generación, con el fin de aprovechar las energías presentes en el ambiente y convertirlas en energía eléctrica, el sistema cuenta con dos salidas de voltaje. , 9 V y 5 V, que servirán como fuente de alimentación para diferentes aplicaciones. La metodología utilizada consta de 4 etapas en las que se muestra el diseño, simulación, fabricación y caracterización de las etapas que conforman el sistema. Las pruebas operativas demostraron que el sistema funciona como se indica, durante el día el sistema puede cargar completamente una batería de 9 V a 250 mA en aproximadamente 3 h, mientras que la energía total recolectada durante una noche completa fue de 560 mV. Las salidas de voltaje varían entre 8,86 V y 5,04 V respectivamente cuando la batería se está cargando y 9,11 V y 5,16 V respectivamente cuando la batería está completamente cargada. Este trabajo tiene como objetivo sentar las bases para futuras investigaciones sobre sistemas híbridos de recolección de energía. 

Palabras clave: Cosecha de energía · Terminales 5G · Sistema híbrido · Solar · Radiofrecuencia 1 

Introducción

 En los últimos años, el uso de energías limpias ha ido aumentando paulatinamente, debido a la necesidad de reducir las emisiones de carbono y la contaminación generada por las fuentes de energía tradicionales [1], diferentes Los estudios se han centrado en la generación de energía a partir de fuentes renovables [2] y que no suponen un impacto significativo en el medio ambiente, como la energía solar y la energía eólica [3], que actualmente se están utilizando para aplicaciones a gran escala como el suministro de energía. electricidad a ciudades o industrias [4]. De esta premisa nace la tecnología conocida como Energy Harvesting, donde surge la posibilidad de aprovechar la energía presente en el ambiente y transformarla en energía eléctrica, capaz de alimentar dispositivos electrónicos de bajo consumo como sensores inalámbricos, teléfonos celulares, terminales IoT, entre otros. otros [5, 6]. Últimamente se han desarrollado varias investigaciones centradas en la recolección de energía como se muestra en los artículos: “A Survey on Recent Energy Harvesting Mechanisms”, donde los autores presentan un estudio sobre la recolección de energía electromagnética, electrostática y piezoeléctrica [7] y “Avances recientes y futuros”. perspectivas en tecnologías de recolección de energía”, que describe el desarrollo de materiales, procedimientos y desafíos presentados por las tecnologías de recolección de energía [8]. El uso de la radiofrecuencia como fuente de captación de energía ha sido de gran interés debido a que señales como radio, televisión, celular, wifi, satélite, entre otras, permanecen presentes en el ambiente todo el tiempo [9]. Sin embargo, la energía recolectada por este tipo de sistema es baja, generalmente en el rango de milivoltios como se muestra en: “Antenas logarítmicas para aplicaciones de recolección de energía electromagnética” [10]; “Sistema portátil de recolección de energía electromagnética” [11]; y “Diseño de circuitos de recolección de energía de radiofrecuencia para aplicaciones de electrónica de baja potencia” [12]. Un tipo de sistema de recolección de energía que presenta buenos resultados es el que aprovecha la energía solar, el voltaje recolectado por este tipo de sistema es mayor en comparación con la Radiofrecuencia, como se muestra en “Un sistema eficiente de recolección de energía solar para nodos sensores inalámbricos”. [13],

EMPEIZA NOMBRAD PAPERS DE LOS QUE SE BASO O SACO SU INFORMACION

 sin embargo, estos resultados varían según las horas del día, y durante la noche la captación de energía es nula. Es por esta razón que proponemos el diseño e implementación de un sistema de recolección de energía que combine las ventajas de la radiofrecuencia y los sistemas solares para crear un sistema híbrido eficiente que sea capaz de alimentar continuamente dispositivos 5G IoT de quinta generación. La metodología utilizada para el desarrollo del sistema se divide en 4 etapas:

 la primera describe el proceso de diseño de los elementos que conforman el sistema; 

el segundo muestra las simulaciones realizadas;

 el tercero describe el método de fabricación que se utilizó;

 Finalmente, en la cuarta etapa, se detallan los métodos utilizados para la toma de mediciones. 

2 Metodología 

Los métodos utilizados para el diseño, simulación, fabricación y caracterización de cada etapa del sistema se describen a continuación.

 2.1 Diseño

 El diagrama de bloques del sistema híbrido se muestra en la Fig. 1. Los paneles solares convierten la energía solar en energía eléctrica la cual ingresa al convertidor elevador que se encarga de elevarla al cargador de baterías. entrega el voltaje a la batería de 9V hasta que esté completamente cargada, luego se desconecta, la antena capta las ondas de radiofrecuencia presentes en el ambiente, el multiplicador de voltaje rectifica y eleva el voltaje captado, esta etapa se conecta al cargador de baterías, el selector de voltaje La etapa funciona como un interruptor para mantener constante el voltaje de salida al cambiar entre el voltaje del convertidor elevador y la batería, finalmente la etapa divisora de voltaje reduce la salida de 9 V a 5 V que se puede usar para diferentes aplicaciones. 

Fig. 1. Diagrama de bloques del sistema híbrido de recolección de energía propuesto.

Antena De los varios tipos de antenas existentes para captación de energía, las más utilizadas son las de tipo parche o microstrip, así mismo dentro de este tipo de antenas existen variedad de geometrías como: cuadrada, rectangular, circular, elíptica, triangular, entre otras [ 14]. Para el sistema se propone el diseño de una antena de parche ranurada, y la frecuencia de resonancia se toma como Fr = 2.4 GHz, el material del sustrato es fibra de vidrio FR4, la cual tiene una constante dieléctrica εr = 4.3 y un espesor h = 1.465 mm. Para el cálculo matemático se utilizaron las siguientes ecuaciones. Ancho del parche

 Paneles Solares Para esta etapa se optó por utilizar 4 paneles solares idénticos, cada uno entrega un voltaje de 2.4 V y una corriente de 80 mA cuando trabaja a su máxima capacidad, debido a que el sistema debe contar con la corriente necesaria para alimentar dispositivos 5G de quinta generación y también para cargar la batería se realizó una configuración mixta Serie-Paralelo, la cual se muestra en la Fig. 2. Para la conexión de los paneles solares los cálculos se realizaron con las Ecs. 5 y 6. 

VT = Vpanel1 + Vpanel2 = Vpanel3 + Vpanel4 (5) donde VT = Voltaje total que tendrá el conjunto de paneles solares, debido a que los paneles son idénticos el voltaje que se obtiene sumando Vpanel1 y Vpanel2 es el mismo sumando Vpanel3 y Vpanel4 y como se mantiene el voltaje de dos fuentes en paralelo, este será el voltaje de salida del conjunto de paneles VT = 4.8V. IT = Iserie1 + Iserie2 (6) donde IT = Corriente total del arreglo, debido a que al conectar dos fuentes en serie la corriente se mantiene, la Iserie1 es igual a la corriente del panel en este caso 80 mA, por lo tanto, la IT = 160 mA .

Fig. 2. Conjunto de paneles solares en configuración mixta.

Multiplicador de Voltaje

 Para esta etapa se propone el diseño de un multiplicador de voltaje Cockcroft-Walton de 5 etapas utilizando capacitores electrolíticos de 100 uF y diodos Schottky HSMS286C debido a que presenta mejores resultados para este tipo de aplicaciones que otros diodos como el BAT43 o el 1N5819, como se muestra. en “Sistema de Acondicionamiento para un Dispositivo de Captación de Energía Electromagnética” [15], además de su bajo consumo de aproximadamente 30 mV y rápida respuesta en altas frecuencias. La Figura 3 muestra el multiplicador diseñado en el software Proteus. Convertidor Elevador Para esta etapa se utilizó el convertidor elevador MT3608 debido a sus características tales como: voltaje de entrada de 2 V a 24 V, voltaje de salida ajustable hasta 28 V, limitador de corriente integrado, bajo consumo de corriente, eficiencia de hasta el 97 % y tamaño pequeño, lo que lo hace perfecto para usar en aplicaciones de bajo consumo. El diseño del circuito se basó en el circuito de aplicación básica sugerido en la hoja de datos. Así, se obtuvo el circuito que se muestra en la Fig. 4.

Fig. 3. Diseño del multiplicador de voltaje de 5 etapas Cockcroft-Walton.

Fig. 4. Convertidor elevador diseñado

Cargador de Baterías Para el circuito del cargador de baterías se optó por una configuración sencilla utilizando un relé de 5 V, 2 diodos Schottky 1N5819W, 1 transistor S8050 y un potenciómetro de precisión 1K. La batería se conecta al pin normalmente cerrado del relé, una vez que el voltaje de la batería llega a su carga máxima el relé se activa enviando el voltaje de carga al pin normalmente abierto, con el potenciómetro se puede variar el voltaje máximo de carga que alcanzará la batería. . La Figura 5 muestra el circuito cargador de baterías diseñado en Proteus.

Fig. 5. Circuito cargador de baterías diseñado

Selector de Voltaje Esta etapa fue diseñada para que el voltaje de salida del sistema sea constante, y la batería se use sólo cuando sea necesario, extendiendo así la vida útil de la batería. Se utiliza un transistor Mosfet de canal P como interruptor, una resistencia de 10K y un diodo Schottky. El circuito diseñado se muestra en la Fig. 6. De esta manera, siempre que haya un voltaje positivo en la puerta del Mosfet, el Mosfet permanecerá abierto y el voltaje de salida será el proveniente del convertidor elevador, mientras que si el convertidor elevador El voltaje del convertidor cae, la resistencia Pull-Down conecta a tierra la puerta Mosfet, por lo que se cerrará permitiendo que pase el voltaje de la batería, el diodo Schottky sirve como protección.

Fig. 6. Circuito selector de voltaje diseñado.

Divisor de Voltaje Para tener también una salida de 5 V para aplicaciones que requieran menor voltaje de alimentación, se realiza un circuito divisor de voltaje utilizando dos resistencias, para el cálculo de sus valores Ec. 5 se utiliza donde Vo = voltaje de salida y Vin = voltaje de entrada. Se utiliza un valor de R1 = 1K y el voltaje de entrada Vin = 9V, con este dato se puede reemplazar en la Ec. 5 y borre R2 para calcular su valor. V

Diagrama de Circuito Una vez realizado el diseño de cada etapa del sistema y para optimizar dimensiones, se decidió unificar las etapas de Convertidor Elevador, Cargador de Baterías, Selector de Voltaje y Divisor de Voltaje, en un solo circuito, obteniendo así el circuito que se muestra. en la figura 7.

Fig. 7. Diagrama de los circuitos combinados.

2.2 Antena de Simulación 

Para realizar la simulación de la antena de parche se utiliza el software CST STUDIO SUITE 2019 ya que permite el diseño, análisis y optimización de sistemas electromagnéticos con una alta precisión, además cuenta con las herramientas de simulación necesarias para determinar los resultados requeridos. para el estudio. Ranuras Como se muestra en el artículo “Diseño y análisis de una antena de parche microcinta ranurada, una revisión” [16], agregar ranuras a la geometría de la antena de parche afecta varias propiedades de la antena, como la ganancia, el patrón de radiación, la directividad y la pérdida de retorno, según la forma. número y dimensiones de las ranuras. Otro beneficio es la supresión de armónicos, como se describe en “Una antena de parche rectangular con supresión de armónicos de 2,45 GHz con polarización circular para aplicaciones de transferencia de energía inalámbrica” [17]. Con esta información como base, se realizaron pruebas con diferentes tipos de ranuras hasta llegar al diseño que se muestra en la Fig. 8(a), al ser las esquinas superiores también redondeadas, con este diseño se logró reducir la frecuencia de la segunda armónica hasta 2,43 GHz hasta −16,2 dB, tomando también como referencia un umbral de resonancia de −10 dB, la antena trabajaría desde 2,29 GHz hasta 2,46 GHz. La Figura 8(b), muestra una comparación entre los resultados obtenidos al inicio (línea roja) y una vez insertadas las ranuras (línea verde). 

Paneles Solares

 Para la simulación de los paneles solares se utiliza el software MatLab-Simulink, con el componente PV ARRAY se puede simular un conjunto mixto de paneles, se ingresan los datos característicos de los paneles. Los resultados obtenidos fueron: 4.8V y 160 mA, estos resultados se muestran en la Fig. 9. 2.3 Fabricación de la Antena Para la fabricación de la antena se utiliza el método de plancha, para esto el diseño realizado en 

Fig. 8. a) Antena de parche ranurada de 2,43 GHz diseñada, b) Comparación entre la antena de parche sin ranuras (línea roja) y con ranuras (línea verde). (Figura en color en línea)

Fig. 9. Simulación de conjunto de paneles solares mixtos en MatLab.

CST Studio Suite se exportó a un archivo DXF para luego transformarlo a un archivo de imagen PNG, para finalmente imprimir el diseño y fabricarlo en sustrato FR4. La Figura 10 muestra el resultado de la fabricación de la antena. Finalmente se suelda un conector macho 50- RP-SMA 

Fig. 10. (a) Antena diseñada, (b) Antena fabricada.

Fabricación de Circuitos Una vez diseñados los circuitos en Proteus, se utiliza la herramienta PCB Wizard para diseñar el PCB Layout de cada uno, debido al tamaño de los elementos utilizados, ha sido necesario utilizar herramientas de precisión para la soldadura SMD. La Figura 11 muestra el Layout de PCB diseñado y el resultado de fabricación de los circuitos del sistema diseñado.

Fig. 11. Diseño de PCB y fabricación de a) circuito multiplicador de voltaje, b) sistema completo.

2.4 Caracterización de la Antena

 Para analizar los parámetros de la antena de parche ranurada fabricada se utiliza el analizador de redes vectorial NanoVNA V2, en el que se miden el parámetro S11, S22 y la impedancia de la antena. El analizador debe calibrarse antes de su uso. La Figura 12 muestra el resultado obtenido por el analizador, la frecuencia de resonancia de la antena es de 2.429 GHz a −15.71 dB, estando las frecuencias entre 2.395 GHz y 2.461 GHz por debajo de −10 dB y una impedancia de 50 ohmios a 2.431 GHz. Panel solar El voltaje y la corriente entregados por el conjunto mixto de paneles solares se midieron utilizando un multímetro. Las pruebas se realizaron a las 12:05 horas con cielo completamente despejado, y se obtuvo una tensión medida de 4,51 V y una corriente de 160,4 mA. La Figura 13 muestra los resultados de mediciones prácticas. Multiplicador de Voltaje Para realizar la medición del circuito multiplicador de voltaje, éste debe estar conectado a la antena. Por este motivo se suelda un conector SMA para conectar la antena y el multiplicador. En este caso, por motivos de disponibilidad, se utilizó un conector SMA macho y un adaptador SMA hembra a RP-SMA macho. Las mediciones se realizaron junto a un enrutador Wi-Fi de Huawei. La Figura 14 muestra la medición que resultó en un voltaje máximo de 597 mV

Fig. 12. Gráfica del parámetro S11 medido desde la antena fabricada

Fig. 13. Medidas tomadas del conjunto de paneles solares mixtos: a) tensión medida, b) corriente medida

Fig. 14. Tensión medida en la salida del multiplicador de tensión de 5 etapas.

Convertidor Elevador Utilizando un multímetro se verifica el funcionamiento del convertidor elevador diseñado, encontrando que el circuito comienza a funcionar a partir de 1.8 V. Como se muestra en la Fig. 15, el circuito alcanza un voltaje de salida máximo de 29.5 V cuando 2 Se suministra V a su entrada. A partir de aquí no se registrarán cambios en la salida del circuito a pesar de aumentar el voltaje de entrada.

Fig. 15. a) tensión de entrada, b) tensión de salida del convertidor elevador.

Sistema Implementado Una vez verificado el funcionamiento de cada uno de los circuitos que componen el sistema, se conectan entre sí según el diagrama de bloques que se muestra en la Fig. 1. El sistema completo se muestra en la Fig. 16. Durante el día, la mayor cantidad de energía se obtendrá de los paneles solares, mientras que, por la noche, la antena será la que proporcione el voltaje al circuito.

Fig. 16. Sistema Híbrido de Captación de Energía Solar-Radiofrecuencia para Terminales 5G de Quinta Generación. a) Paneles solares, b) Antena, circuitos y batería.

3 Análisis de Resultados

 Una vez verificado el funcionamiento de cada una de las etapas, se realizaron pruebas de almacenamiento de energía utilizando una batería de 9V a 250 mA y un Condensador de 1000 uF a 50V, en tres ambientes diferentes: junto a un router Wi-Fi, en el jardín de una casa ubicada en el casco urbano y en los jardines de la Universidad Técnica de Ambato (UTA). 

En la Tabla 1. Se muestran los resultados de las mediciones del voltaje captado por la antena, como se puede observar la antena recolectó más voltaje al colocarla cerca de una fuente de radiación de 2.4 GHz como lo es el Router Wi-Fi. 

Tabla 1. Energía Cosechada por la Antena en una batería recargable de 9V.

Se realizaron pruebas con los paneles solares, las mediciones se tomaron en un día soleado y en un día nublado, de esta manera se puede determinar cómo influye el clima en la cantidad de energía almacenada en cada momento. Como se muestra en la Tabla 2, el nivel de voltaje de los paneles en un día soleado como en un día nublado no presenta una diferencia significativa, sin embargo, en un día soleado el voltaje total recolectado es mucho mayor debido a que la corriente entregada por los paneles es directamente proporcional a la cantidad de luz que les incide, por lo que la batería se carga más rápidamente, en este caso la batería recolectó 1.22V en 90. 

Tabla 2. Energía cosechada por los Paneles Solares en una batería recargable de 9V.

En la Tabla 3 se muestran los resultados de las mediciones tomadas con el sistema completo, estas pruebas se realizaron en una zona urbana tanto en un día soleado como nublado y durante la noche. Se puede observar como la energía total recolectada durante el día es muy similar a los resultados de la Tabla 2, obtenidos con los paneles solares, mientras que para la noche el voltaje total recolectado en un periodo de 90 min alcanzó los 110 mV, adicionalmente la energía total recolectada en un periodo de 90 min alcanzó los 110 mV. Se midió recolectada en un periodo de 11 h de 7pm a 6am obteniendo un voltaje de 560mV. También se demostró que durante el día el sistema puede cargar completamente una batería de 9 V a 250 mA en aproximadamente 180 minutos, independientemente de si el día está nublado o soleado.

Finalmente, se calibró la etapa del cargador de baterías para que se desconecte automáticamente cuando el voltaje de la batería alcance los 9.25V, protegiendo así la batería de sobrecargas que podrían reducir su vida útil. Además, se encontró que cuando los paneles solares no alcanzan los 2V requeridos para el funcionamiento del Convertidor Elevador, el voltaje de salida cambia automáticamente al voltaje de la batería, esta transición se realiza casi de inmediato debido a la velocidad del Mosfet. Se utiliza para la etapa selectora de voltaje, de modo que los dispositivos que están conectados al sistema no lo noten. Se tomaron medidas de las salidas de voltaje, comprobando que cuando el sistema está cargando la batería el voltaje en la salida de 9V es de 8.86V mientras que en la salida de 5V es de 5.04V, mientras que una vez que la batería está completamente cargada el voltaje en las salidas es de 9.11 V y 5.16V respectivamente, estos resultados se pueden ver en la Fig. 17.

Fig. 17. a) voltaje medido en la salida de 9 V del sistema, b) voltaje medido en la salida de 5 V del sistema.

El sistema ha sido diseñado para dispositivos 5G, debido a los requerimientos para la ejecución del proyecto de investigación “Captación de Energía Limpia de Baja Potencia para Alimentación de Dispositivos de Quinta Generación (5G)”, que se lleva a cabo. Sin embargo, se puede utilizar para otro tipo de dispositivos como teléfonos celulares, si la energía requerida no es mayor a la que entrega el sistema, 9V y 160 mA aproximadamente.

4 Conclusiones 

En este trabajo se ha llevado a cabo el diseño, simulación, fabricación y caracterización de cada una de las etapas de un sistema híbrido de captación de energía solar-radiofrecuencia para terminales 5G de quinta generación. A través de mediciones y pruebas se verificó que el sistema propuesto funciona según lo diseñado, manteniendo voltajes de 8.86 V y 5.04 V en sus salidas cuando la batería se encuentra cargando y 9.11V y 5.16V cuando la batería deja de cargarse. Los tiempos de carga pueden variar dependiendo de las condiciones climáticas, la hora del día y la distancia del sistema a una fuente de RF, pero se ha descubierto que durante el día la batería se puede cargar completamente en aproximadamente 3 h. La energía captada por la antena no llega a los 2 V requeridos por el convertidor elevador, por lo que se ha optado por conectarlo directamente a la etapa de carga de la batería, esto será útil durante las noches ya que según los resultados obtenidos podría recoge alrededor de 560 mV. El sistema se puede utilizar para alimentar dispositivos de bajo consumo como sensores inalámbricos o terminales basados en tecnología 5G, también se puede calibrar para su uso con baterías de diferentes voltajes, utilizando los dos potenciómetros de precisión ubicados en el PCB principal, siendo el primero el Se regula el voltaje de salida del convertidor elevador, mientras que el segundo se utiliza para indicar el voltaje del relé que se activará para detener la carga de la batería. 

Expresiones de gratitud. 

Los autores agradecen a la Universidad Técnica de Ambato y a la Dirección de Investigación y Desarrollo (DIDE) por su apoyo en la realización de esta investigación, en la ejecución del proyecto "Captación de Energía Limpia de Baja Potencia para Alimentación de Dispositivos de Quinta Generación". (5G)”, aprobado mediante resolución “Nro. UTA-CONIN-2022-0015-R”. Código de proyecto: SFFISEI 07. 

Referencias

1. Li, Y., Chiu, Y.H., Lin, T.Y.: Research on new and traditional energy sources in OECD countries. Int. J. Environ. Res. Public Health 16(7), 1122 (2019). https://doi.org/10.3390/ije rph16071122 

2. Blazu, R., Blachut, J., Ciepiela, A., Labuz, R., Papiez, R.: Renewable energy sources vs. an air quality improvement in urbanized areas – the metropolitan area of kraków case. Front. Energy Res. 9(767418), 1–11 (2021). https://doi.org/10.3389/fenrg.2021.767418 

3. Asantewaa, P., Asumadu-Sarkodie, S.: A review of renewable energy sources, sustainability issues and climate change mitigation. Cogent Eng. 3(1), 1–14 (2016). https://doi.org/10.1080/ 23311916.2016.1167990 

4. Perea, M., Escobedo, Q., Perea, A.: Renewable energy in Urban Areas: worldwide research trends. Energies 11(3), 1–19 (2018). https://doi.org/10.3390/en11030577 

5. Tony, A., Hiryanto, L.: A review on energy harvesting and storage for rechargeable wireless sensor networks. IOP Conference Series: Materials Science and Engineering. 508, 1-11 (2019) 

6. Pop, A., Pop, P., Tihomir, L., Barz, C.: Research about harvesting energy devices and storage method. Open conference systems, innovative ideas in science 4(2), pp. 102–120 (2015) 

7. Abdul-Rahman, K., Mohammad, S.: A survey on recent energy harvesting mechanisms. In: IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), pp. 1–5 (2016). https://doi.org/10.1109/CCECE.2016.7726698 

8. Akinaga, H.: Recent advances and future prospects in energy harvesting technologies. Jpn. J. Appl. Phys. 59(110201), 1–10 (2020) Hybrid Solar-Radiofrequency Energy Harvesting System 17 

9. Hassani, S., Hassani, H., Boutammachte, N.: Overview on 5G radio frequency energy harvesting. Adv. Sci. Technol. Eng. Syst. J. 4(4), 328–346 (2019). https://doi.org/10.25046/aj0 40442 

10. Gordón, C., Freire, E., Brito, G., Salazar, F.: Logarithmic antennas for electromagnetic energy harvesting applications. In: Botto-Tobar, M., Zambrano Vizuete, M., Diaz Cadena, A., Vizuete, A.Z. (eds.) Latest Advances in Electrical Engineering, and Electronics. Lecture Notes in Electrical Engineering, vol 933. Springer, Cham (2022). https://doi.org/10.1007/ 978-3-031-08942-8_17 

11. Cuji, J., Mendoza, L., Brito, G., Gordón, C.: Portable electromagnetic energy harvesting system. In: Chauvin, M.I.A., Botto-Tobar, M., Díaz Cadena, A., Montes León, S. (eds.) CSECity. LNNS, vol. 379, pp. 81–91. Springer, Cham (2022). https://doi.org/10.1007/978- 3-030-94262-5_8 

12. Banerjee, J., Banerjee, S.: Radio frequency energy harvesting circuits design for the applications of low power electronics. Int. J. Electron. Lett. 10(12), (2021) https://doi.org/10.1080/ 21681724.2020.1870719 

13. Sharma, H., Haque, A., Jaffery, Z.: An efficient solar energy harvesting system for wireless sensor nodes. In: 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), pp. 461–464 (2018). https://doi.org/10.1109/ICPEICES. 2018.8897434 

14. Balanis, C.: Antenna Theory Analysis and Design, 2nd edn. Jhon Wiley & Sons, Inc., Ney York (2017) 

15. Balarezo, D., Gordón, C., Cuji, J., Salazar, F.: Conditioning System for an Electromagnetic Energy Collection Device. In: Garcia, M.V., Fernández-Peña, F., Gordón-Gallegos, C. (eds) Advances and Applications in Computer Science, Electronics, and Industrial Engineering. CSEI 2021. Lecture Notes in Networks and Systems, vol 433. Springer, Cham (2022). https:// doi.org/10.1007/978-3-030-97719-1_13 

16. Thangjam, R., Bhattacharyya, K.: Design and analysis of slotted microstrip patch antenna. A review. J. Telecommun. Study 4(2), 1–17 (2018) 

17. Nurzaimah, Z., Zahriladha, Z., Maisarah, A., Mawarni, M.: A 2.45 GHz harmonic suppression rectangular patch antenna with circular polarization for wireless power transfer application. IETE J. Res. 64(3), 310–316 (2018). https://doi.org/10.1080/03772063.2017.1355751

Sistemas Embedidos: VLSI una Guia para estudiantes de Ingenieria

 Maquinas secuenciales

Compuertas logicas en integrados

Maquina de Mealy

Maquina de Moore

Microprocesadores

Arduino 

ESP32

PIC

CUIDADO, Las 18F Requieren que este conectado los 6 pines del PICkit, puede conectarlos por medio de protoboard y ver su correcta coneccion con el software, use de referencia el Datasheep.

 

Xilinx

El Lenguaje de descripcion de Hardware fue hecho para ser facil de usar

El contador puede hacerse simplementa con el codigo "+1"

National Instruments

ELVIS

DAQ

FPGA

SBRio

Bibliografia

https://www.youtube.com/playlist?list=PLONPO-iVba9nbY_KTCHt9GGj9dGSj1qYo

https://www.youtube.com/watch?v=KfFCfUTX4Nk

https://www.youtube.com/@patsvb77

Procesamiento de señales digitales de Monson H. Hayes - LIBRO EN ESPAÑOL

 El límite de Schaum

Procesamiento de señales digitales

Monson H. Hayes

la ayuda perfecta para sacar mejores notas¡

Cubre todos los fundamentos del curso: complementa cualquier texto de clase

profesor de resolución de problemas eficaz

más de 300 problemas resueltos paso a paso

Ideal para estudio independiente.

Esquema de teoría y problemas de Schaum

 Procesamiento de señales digitales

 Monson h hayes

Catedrático de Ingeniería Eléctrica e Informática

Instituto de Tecnología de Georgia

SERIE ESQUEMA DE SCHAUM

MONSON H. HAYES es profesor de Ingeniería Eléctrica e Informática en Georgia

Instituto de Tecnología de Atlanta, Georgia. Recibió su B.A. Licenciado en Física por la Universidad de California, Berkeley, y su M.S.E.E. y Sc.D. grados en ingeniería eléctrica y Ciencias de la Computación del M.I.T. Sus intereses de investigación se centran en el procesamiento de señales digitales con aplicaciones en procesamiento de imagen y video. Ha contribuido con más de 100 artículos a revistas y actas de congresos, y es el autor del libro de texto Statistical Digital Signal Processing and Modeling, John Wiley & Sons, 1996. Recibió el IEEE Senior Award como autor de un artículo de mérito excepcional de la ASSP Society of the IEEE en 1983, el Presidential Young Investigator Award en 1984, y fue elegido para el grado de Fellow del IEEE en 1992 por su "contribuciones al modelado de señales, incluido el desarrollo de algoritmos para la restauración de señales de la fase o magnitud de la transformada de Fourier". 

Esquema de teoría y problemas de Schaum

PROCESAMIENTO DE SEÑALES DIGITALES

Copyright © 1999 de The McGraw-Hill Companies, Inc. Todos los derechos reservados. Impreso en los Estados Unidos Estados de América. Salvo lo permitido por la Ley de derechos de autor de 1976, ninguna parte de esta publicación puede ser reproducida o distribuida en cualquier forma o por cualquier medio, o almacenada en una base de datos o recuperación sistema, sin el permiso previo por escrito del editor.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 PRS PRS 9 0 2 10 9

ISBN 0–07–027389–8

Editor patrocinador: Barbara Gilson

Supervisora de Producción: Pamela Pelton

Supervisora de edición: Maureen B. Walker

Datos de catalogación en publicación de la Biblioteca del Congreso

Hayes, M. H. (Monson H.), fecha.

 Esquema de Schaum de la teoría y los problemas de la señal digital.

 procesamiento / Monson H. Hayes.

 pag. cm. - (Serie de esquemas de Schaum)

Incluye índice.

 ISBN 0–07–027389–8

 1. Procesamiento de señales—Técnicas digitales—Problemas, ejercicios, etc. 2. Procesamiento de señales—Técnicas digitales—Resúmenes, planes de estudio, etc. I. Título. II. Título: Teoría y problemas de la señal digital  

Procesando.

 TK5102.H39 1999

 621.382'2—dc21 98–43324

 CIP

Para Arenita

Prefacio

El procesamiento de señales digitales (DSP) se ocupa de la representación de señales en forma digital, y

con el procesamiento de estas señales y la información que llevan. Aunque DSP, como sabemos hoy, comenzó a florecer en la década de 1960, algunas de las técnicas de procesamiento importantes y poderosas que están en uso hoy en día se remontan a algoritmos numéricos que fueron propuestos y estudiados hace siglos. Desde principios de la década de 1970, cuando se introdujeron los primeros chips DSP, el campo de la digitalización

 El procesamiento de señales ha evolucionado dramáticamente. Con un aumento tremendamente rápido en la velocidad de DSP procesadores, junto con un aumento correspondiente en su sofisticación y poder computacional, El procesamiento de señales digitales se ha convertido en una parte integral de muchos productos y aplicaciones comerciales, y se está convirtiendo en un término común. 

Este libro se ocupa de los fundamentos del procesamiento de señales digitales, y hay dos maneras que el lector puede usar este libro para aprender sobre DSP. En primer lugar, puede utilizarse como complemento de cualquier uno de una serie de excelentes libros de texto de DSP al proporcionar al lector una rica fuente de trabajo problemas y ejemplos. Alternativamente, puede usarse como una guía de autoaprendizaje de DSP, usando el método de aprender con el ejemplo. Con cualquier enfoque, este libro ha sido escrito con el objetivo de proporcionar al lector con una amplia gama de problemas con diferentes niveles de dificultad. Además de problemas que pueden considerarse ejercicios, el lector encontrará problemas más desafiantes que requieren  cierta creatividad en su solución, así como problemas que exploran aplicaciones prácticas como calcular los pagos de una hipoteca de vivienda. Cuando es posible, un problema se trabaja en varios se sugieren diferentes formas o métodos alternativos de solución.

Los nueve capítulos de este libro cubren lo que normalmente se considera el material central para un Curso introductorio en DSP. El primer capítulo presenta los conceptos básicos del procesamiento de señales digitales y sienta las bases para el material de los siguientes capítulos. Los temas tratados en este capítulo incluyen la descripción y caracterización de señales y sistemas de tipo discreto, convolución y ecuaciones diferenciales de coeficientes constantes lineales. El segundo capítulo considera la representación de señales de tiempo discreto en el dominio de la frecuencia. Específicamente, presentamos el Fourier de tiempo discreto transformar (DTFT), desarrollar una serie de propiedades de DTFT y ver cómo se puede usar el DTFT para resolver ecuaciones en diferencias y realizar convoluciones. El capítulo 3 cubre los temas importantes  asociado con el muestreo de señales de tiempo continuo. De primordial importancia en este capítulo es la teorema de muestreo y la noción de aliasing. En el Capítulo 4, se desarrolla la transformada z, que es el equivalente en tiempo discreto de la transformada de Laplace para señales en tiempo continuo. Luego, en el Capítulo 5, observamos la función del sistema, que es la transformada z de la respuesta de la muestra unitaria de un sistema lineal

sistema de cambio invariante, e introducir una serie de diferentes tipos de sistemas, como allpass, linear

filtros de fase y fase mínima, y sistemas de realimentación. Los siguientes dos capítulos se ocupan de la transformada discreta de Fourier (DFT). En el capítulo 6, nos introducir la DFT y desarrollar una serie de propiedades de la DFT. La idea central de este capítulo es que multiplicar las DFT de dos secuencias corresponde a la convolución circular en el dominio del tiempo.

Luego, en el Capítulo 7, desarrollamos una serie de algoritmos eficientes para calcular la DFT de una secuencia de longitud finita. Estos algoritmos se denominan, genéricamente, transformadas rápidas de Fourier (FFT). 

Finalmente, los últimos dos capítulos consideran el diseño e implementación de sistemas de tiempo discreto. En En el Capítulo 8, analizamos diferentes formas de implementar un sistema de tiempo discreto invariante con desplazamiento lineal, y mire la sensibilidad de estas implementaciones para filtrar la cuantificación del coeficiente. Además, nosotros analizar la propagación del ruido de redondeo en implementaciones de punto fijo de estos sistemas. Luego, en el Capítulo 9, veremos técnicas para diseñar filtros invariantes de desplazamiento lineal FIR e IIR. Aunque el enfoque principal está en el diseño de filtros de paso bajo, también se consideran técnicas para diseñar otros filtros selectivos de frecuencia, como filtros de paso alto, de paso de banda y de supresión de banda. Se espera que este libro sea una herramienta valiosa para aprender DSP. Las opiniones y los comentarios son bienvenidos a través del sitio web de este libro, que se puede encontrar en http://www.ee.gatech.edu/users/mhayes/schaum. También estará disponible en este sitio información importante, como correcciones o ampliaciones. a los problemas de este libro, lecturas y problemas adicionales y comentarios de los lectores.

Contenido 

Capítulo 1. Señales y Sistemas 1

 

1.1 Introducción 1

 

1.2 Señales de tiempo discreto 1

 

1.2.1 Secuencias complejas 2

 

1.2.2 Algunas secuencias fundamentales 2

 

1.2.3 Duración de la señal 3

 

1.2.4 Secuencias periódicas y aperiódicas 3

 

1.2.5 Sucesiones simétricas 4

 

1.2.6 Manipulaciones de señales 4

 

1.2.7 Descomposición de la señal 6

 

1.3 Sistemas de tiempo discreto 7

 

1.3.1 Propiedades de los sistemas 7

 

1.4 Convolución 11

 

1.4.1 Propiedades de convolución 11

 

1.4.2 Realización de circunvoluciones 12

 

1.5 Ecuaciones en diferencias 15

 

Problemas Resueltos 18

 

Capítulo 2. Análisis de Fourier 55

 

2.1 Introducción 55

 

2.2 Respuesta de frecuencia 55

 

2.3 Filtros 58

 

2.4 Interconexión de Sistemas 59

 

2.5 La transformada de Fourier en tiempo discreto 61

 

2.6 Propiedades DTFT 62

 

2.7 Aplicaciones 64

 

2.7.1 Sistemas LSI y LCCDE 64

 

2.7.2 Realización de circunvoluciones 65

 

2.7.3 Resolver ecuaciones en diferencias 66

 

2.7.4 Sistemas Inversos 66

 

Problemas Resueltos 67

 

Capítulo 3. Muestreo 101

 

3.1 Introducción 101

 

3.2 Conversión de analógico a digital 101

 

3.2.1 Muestreo periódico 101

 

3.2.2 Cuantización y codificación 104

 

3.3 Conversión de digital a analógico 106

 

3.4 Procesamiento en tiempo discreto de señales analógicas 108

 

3.5 Conversión de frecuencia de muestreo 110

 

3.5.1 Reducción de la frecuencia de muestreo por un factor entero 110

 

3.5.2 Aumento de la frecuencia de muestreo por un factor entero 111

 

3.5.3 Conversión de frecuencia de muestreo por un factor racional 113

 

Problemas Resueltos 114

 

Capítulo 4. La transformación Z 142

 

4.1 Introducción 142

 

4.2 Definición de la transformada z 142

 

4.3 Propiedades 146

 

4.4 La transformada z inversa 149

 

4.4.1 Expansión de fracciones parciales 149

 

4.4.2 Serie de potencia 150

 

4.4.3 Integración de contornos 151

 

4.5 La transformada z unilateral 151

 

Problemas Resueltos 152

 

Capítulo 5. Análisis transformado de sistemas 183

 

5.1 Introducción 183

 

5.2 Función del sistema 183

 

5.2.1 Estabilidad y causalidad 184

 

5.2.2 Sistemas inversos 186

 

5.2.3 Respuesta de muestra unitaria para funciones de sistemas racionales 187

 

5.2.4 Respuesta de frecuencia para funciones de sistemas racionales 188

 

5.3 Sistemas con fase lineal 189

 

5.4 Filtros paso total 193

 

5.5 Sistemas de fase mínima 194

 

5.6 Sistemas de retroalimentación 195

 

Problemas Resueltos 196

 

Capítulo 6. El DFT 223

 

6.1 Introducción 223

 

6.2 Serie discreta de Fourier 223

 

6.3 Transformada de Fourier discreta 226

 

6.4 Propiedades DFT 227

 

6.5 Muestreo del DTFT 231

 

6.6 Convolución lineal usando el DFT 232

 

Problemas Resueltos 235

 

Capítulo 7. La transformada rápida de Fourier 262

 

7.1 Introducción 262

 

7.2 Algoritmos Radix-2 FFT 262

 

7.2.1 Decimación en el tiempo FFT 262

 

7.2.2 FFT de diezmado en frecuencia 266

 

7.3 Algoritmos FFT para compuesto N 267

 

7.4 Factor primo FFT 271

 

Problemas Resueltos 273

 

Capítulo 8. Implementación de sistemas de tiempo discreto 287

 

8.1 Introducción 287

 

8.2 Redes digitales 287

 

8.3 Estructuras para sistemas FIR 289

 

8.3.1 Formulario Directo 289

 

8.3.2 Cascada Formulario 289

 

8.3.3 Filtros de fase lineal 289

 

8.3.4 Muestreo de frecuencia 291

 

8.4 Estructuras para sistemas IIR 291

 

8.4.1 Formulario Directo 292

 

8.4.2 Cascada Forma 294

 

8.4.3 Estructura paralela 295

 

8.4.4 Estructuras transpuestas 296

 

8.4.5 Filtros paso total 296

 

8.5 Filtros de celosía 298

 

8.5.1 Filtros de celosía FIR 298

 

8.5.2 Filtros de red de todos los polos 300

 

8.5.3 Filtros de celosía IIR 301

 

8.6 Efectos de longitud de palabra finita 302

 

8.6.1 Representación binaria de números 302

 

8.6.2 Cuantización de coeficientes de filtro 304

 

8.6.3 Ruido de redondeo 306

 

8.6.4 Emparejamiento y pedidos 309

 

8.6.5 Desbordamiento 309

 

Problemas Resueltos 310

 

Capítulo 9. Diseño de filtros 358

 

9.1 Introducción 358

 

9.2 Especificaciones del filtro 358

 

9.3 Diseño de filtro FIR 359

 

9.3.1 Diseño FIR de fase lineal con Windows 359

 

9.3.2 Diseño de filtro de muestreo de frecuencia 363

 

9.3.3 Filtros de fase lineal Equiripple 363

 

9.4 Diseño de filtro IIR 366

 

9.4.1 Prototipos de filtro de paso bajo analógico 367

 

9.4.2 Diseño de filtros IIR a partir de filtros analógicos 373

 

9.4.3 Transformaciones de frecuencia 376

 

9.5 Diseño de filtros basado en un enfoque de mínimos cuadrados 376

 

9.5.1 Aproximación de pad 377

 

9.5.2 Método de Prony 378

 

9.5.3 Inversa de mínimos cuadrados FIR 379

 

Problemas Resueltos 380

 

Índice 429

Capítulo 1 Señales y Sistemas

1.1INTRODUCCIÓN

En este capítulo comenzamos nuestro estudio del procesamiento de señales digitales desarrollando la noción de una señal en tiempo discreto. y un sistema de tiempo discreto. Nos concentraremos en resolver problemas relacionados con representaciones de señales, manipulaciones, propiedades de las señales, clasificación del sistema y propiedades del sistema. Primero, en la Sec. 1.2 definimos exactamente lo que significa una señal de tiempo discreto y luego desarrollar algunas operaciones básicas, pero importantes, que se puede realizar en estas señales. Luego, en la Sec. 1.3 consideramos sistemas de tiempo discreto. De especial importancia serán las nociones de linealidad, cambio-invariancia, causalidad, estabilidad e invertibilidad. Se demostrará que para sistemas que son lineales e invariantes al cambio, la entrada y la salida están relacionadas por una suma de convolución. Propiedades de la suma de convolución y los métodos para realizar convoluciones se discuten en la Sec. 1.4. Finalmente, en la Sec. 1.5 observamos sistemas de tiempo discreto que se describen en términos de una ecuación de diferencia.

1.2 SEÑALES DE TIEMPO DISCRETO

Una señal de tiempo discreto es una secuencia indexada de números reales o complejos. Por lo tanto, una señal en tiempo discreto es una función de una variable de valor entero, n, que se denota por x(n). Aunque la variable independiente n no necesita representan necesariamente "tiempo" (n puede, por ejemplo, corresponder a una coordenada espacial o distancia), x(n) es generalmente referido como una función del tiempo. Una señal de tiempo discreto no está definida para valores no enteros de n. Por lo tanto, unla señal de valor real x(n) se representará gráficamente en forma de diagrama de piruleta como se muestra en la Fig. 1-I. En  algunos problemas y aplicaciones es conveniente ver x(n) como un vector. 

Figura 1-1. La representación gráfica de una señal de tiempo discreto x(n).

Por lo tanto, la secuencia de valores x(0) a x(N - 1) a menudo se puede considerar como los elementos de un vector columna de la siguiente manera: 

Las señales de tiempo discreto a menudo se obtienen mediante el muestreo de una señal de tiempo continuo, como el habla, con un convertidor de analógico a digital (AID). Por ejemplo, una señal de tiempo continuo x,(t) que se muestrea a una tasa de fs = l/Ts muestras por segundo produce la señal muestreada x(n), que se relaciona con xa(t) de la siguiente manera:  

Sin embargo, no todas las señales de tiempo discreto se obtienen de esta manera. Algunas señales pueden considerarse naturalmente secuencias de tiempo discreto que ocurren porque no hay un convertidor físico de analógico a digital que esté convirtiendo una señal analógica en una señal de tiempo discreto. Ejemplos de señales que caen en esta categoría incluyen acciones diarias: precios de mercado, estadísticas de población, inventarios de almacenes y el número de manchas solares de Wolfer^.^

1.2.1 Secuencias complejas

En general, una señal de tiempo discreto puede tener un valor complejo. De hecho, en una serie de aplicaciones importantes como comunicaciones digitales, las señales complejas surgen naturalmente. Una señal compleja puede expresarse en términos de sus partes real e imaginaria, 

o en forma polar en términos de su magnitud y fase,

La magnitud se puede derivar de las partes real e imaginaria de la siguiente manera

mientras que la fase se puede encontrar usando

Si z(n) es una secuencia compleja, el conjugado complejo, denotado por z*(n), se forma cambiando el signo en la

parte imaginaria de z(n):

1.2.2 Algunas secuencias fundamentales

Aunque la mayoría de las señales portadoras de información de interés práctico son funciones complicadas del tiempo, hay tres señales de tiempo discreto simples, pero importantes, que se utilizan con frecuencia en la representación y descripción de más señales complicadas. Estos son la muestra unitaria, el escalón unitario y el exponencial. La muestra unitaria, denotada por S(n), está definido por

y juega el mismo papel en el procesamiento de señales de tiempo discreto que el impulso unitario juega en la señal de tiempo continuo Procesando. El escalón unitario, denotado por u(n), está definido por

 y se relaciona con la muestra unitaria por

De manera similar, una muestra unitaria se puede escribir como una diferencia de dos pasos:

El número R de manchas solares de Wolfer fue introducido por Rudolf Wolf en 1848 como una medida de la actividad de las manchas solares. Los registros diarios están disponibles atrás hasta 1818 y se han hecho estimaciones de medias mensuales desde 1749. Ha habido mucho interés en estudiar la correlación entre actividad de manchas solares y fenómenos terrestres como datos meteorológicos y variaciones climáticas. 

Finalmente, una sucesión exponencial está definida por

 donde a puede ser un número real o complejo. De particular interés es la secuencia exponencial que se forma cuando a = e~m, donde q, es un número real. En este caso, x(n) es una exponencial compleja

 Como veremos en el próximo capítulo, las exponenciales complejas son útiles en la descomposición de señales de Fourier.

1.2.3 Duración de la señal

Las señales de tiempo discreto pueden clasificarse convenientemente en términos de su duración o extensión. Por ejemplo, se dice que una secuencia de tiempo discreto es una secuencia de longitud finita si es igual a cero para todos los valores de n fuera de una secuencia finita.

intervalo [N1, N2]. Las señales que no tienen una longitud finita, como el escalón unitario y el exponencial complejo, se dice ser secuencias de longitud infinita. Las secuencias de longitud infinita pueden clasificarse además como del lado derecho, lado izquierdo o de dos lados. Una secuencia del lado derecho es cualquier secuencia de longitud infinita que es igual a cero para todos los valores de n < no para algún número entero. El paso unitario es un ejemplo de una secuencia del lado derecho. Del mismo modo, una longitud infinita 

Se dice que la secuencia x(n) es de lado izquierdo si, para algún número entero no, x(n) = 0 para todo n > no. Un ejemplo de izquierda la secuencia es

que es un paso unitario retardado e invertido en el tiempo. Una señal de longitud infinita que no es ni del lado derecho ni del lado izquierdo, como el exponencial complejo, se conoce como una secuencia de dos colas.

1.2.4 Secuencias periódicas y aperiódicas

Una señal de tiempo discreto siempre se puede clasificar como periódica o aperiódica. Se dice que una señal x(n) es periódica si, para algún entero real positivo N, 

 para todos Esto equivale a decir que la secuencia se repite cada N muestras. Si una señal es periódica con  período N, también es periódico con período 2N, período 3N y todos los demás múltiplos enteros de N. El fundamental período, que denotaremos por N, es el entero positivo más pequeño para el cual la ecuación. (I .I) está satisfecho. Si la ecuación. (1 .I)

no se cumple para ningún número entero N, se dice que x(n) es una señal aperiódica.

EJEMPLO 1.2.1 Las señales

 y

 

no son periódicas, mientras que la señal.

 

es periódico y tiene un período fundamental de N = 16.  Si xl(n) es una sucesión periódica con un período N1, y x2(n) es otra sucesión periódica con un período N2, la suma 

siempre será periódica y el periodo fundamental es

 donde mcd(NI, N2) significa el máximo común divisor de N1 y N2. Lo mismo es cierto para el producto; eso es 

será periódico con un período N dado por la ecuación. (1.2). Sin embargo, el período fundamental puede ser menor. 

Dada cualquier secuencia x(n), siempre se puede formar una señal periódica replicando x(n) de la siguiente manera:

  donde N es un entero positivo. En este caso, y(n) será periódica con periodo N.

1.2.5 Secuencias simétricas

Una señal de tiempo discreto a menudo poseerá alguna forma de simetría que puede aprovecharse para resolver problemas.

Dos simetrías de interés son las siguientes:

Definición: Se dice que una señal de valor real es par si, para todo n,

x(n) = x(-n)

mientras que se dice que una señal es impar si, para todo n,

x(n) = -x(-n)

Cualquier señal x(n) puede descomponerse en la suma de su parte par, x,(n), y su parte impar, x,(n), como sigue:

 

Para encontrar la parte par de x(n) formamos la suma x,(n) = (1/2)(x(n)+x(-n)) 

mientras que para encontrar la parte impar tomamos la diferencia x,(n) = i(x(n)-x(-n)) 

Para secuencias complejas, las simetrías de interés son ligeramente diferentes.

Definición: Se dice que una señal compleja es simétrica conjugada3 si, para todo n, x(n) = x*(-n) 

y se dice que una señal es antisimétrica conjugada si, para todo n,

x(n) = -x*(-n) 

Cualquier señal compleja siempre se puede descomponer en la suma de una señal simétrica conjugada y una señal conjugada señal antisiméuica.

1.2.6 Manipulaciones de señales

En nuestro estudio de señales y sistemas de tiempo discreto nos ocuparemos de la manipulación de señales. Estos las manipulaciones son generalmente composiciones de unas pocas transformaciones de señal básicas. Estas transformaciones pueden ser clasificados como aquellos que son transformaciones de la variable independiente n o aquellos que son transformaciones de la amplitud de x(n) (es decir, la variable dependiente). En las dos subsecciones siguientes veremos brevemente estas dos clases de transformaciones y enumere las que se encuentran más comúnmente en las aplicaciones

A veces se dice que una secuencia que es simétrica conjugada es hermítica.

Transformaciones de la Variable Independiente

Las secuencias a menudo se alteran y manipulan modificando el índice n de la siguiente manera:

donde f (n) es alguna función de n. Si, para algún valor de n, f (n) no es un número entero, y(n)= x(f(n)) no está definido. La determinación del efecto de modificar el índice n siempre se puede lograr utilizando un enfoque tabular simple de listar, para cada valor de n, el valor de f (n) y luego establecer y(n) = x( f (n)). Sin embargo, para muchos índices transformaciones esto no es necesario, y la secuencia se puede determinar o trazar directamente. Los más comunes Las transformaciones incluyen desplazamiento, inversión y escalado, que se definen a continuación.

 Desplazamiento Esta es la transformación definida por f (n) = n -no. Si y(n) = x(n -no), x(n) se desplaza a hacia la derecha por ninguna muestra si no es positivo (esto se conoce como un retraso), y se desplaza a la izquierda por no muestras si no es negativo (lo que se denomina anticipo). 

Inversión Esta transformación viene dada por f (n) = -n y simplemente implica "voltear" la señal x(n)

con respecto al índice n.

Escalado de tiempo Esta transformación se define por f (n) = Mn o f (n) = n/ N donde M y N son

enteros positivos. En el caso de f (n) = Mn, la secuencia x(Mn) se forma tomando cada M-ésima muestra de x(n) (esta operación se conoce como submuestreo). Con f (n) = n/N la secuencia y(n) =x( f (n)) es definido de la siguiente manera:

(esta operación se conoce como sobremuestreo).

En la figura 1-2 se ilustran ejemplos de desplazamiento, inversión y escalado de tiempo de una señal.

(a) Una señal de tiempo discreto.

(h) Un retraso por no = 2.

(c) Inversión del tiempo.

(d) Reducción de muestreo por un factor de 2.

(e) Muestreo ascendente por un factor de 2

Figura 1-2. Ilustración de las operaciones de desplazamiento, inversión y escalado de la variable independiente n.

Las operaciones de desplazamiento, inversión y escalado de tiempo dependen del orden. Por lo tanto, hay que tener cuidado en evaluar las composiciones de estas operaciones. Por ejemplo, la figura 1-3 muestra dos sistemas, uno que consta de un retraso seguido de una reversión y uno que es una reversión seguida de un retraso. Como se indica. las salidas de estos dos sistemas no son lo mismo.

(a) Un retraso Tn, seguido de una inversión de tiempo Tr.

(b) Una inversión de tiempo Tr seguida de un retardo T",,

Figura 1-3. Ejemplo que ilustra que las operaciones de retardo e inversión no

no conmutar

Adición, multiplicación y escalado

Los tipos más comunes de transformaciones de amplitud son la suma, la multiplicación y la escala. realizando estos Las operaciones son sencillas e involucran solo operaciones puntuales en la señal.

Adición La suma de dos señales se forma por la suma puntual de los valores de la señal.

X1(n)+ X2(n) =y(n)

Multiplicación La multiplicación de dos señales está formado por el producto puntual de los valores de la señal.

X1(n) X2(n) =y(n)

Escalado El escalado de amplitud de una señal x(n) por una constante c se logra multiplicando cada

valor de la señal por c:

y(n)=cx(n) -oo<n<oo

Esta operación también puede considerarse como el producto de dos señales, x(n) y f(n)= c

1.2.7 Descomposición de la señal 

 La muestra unitaria puede usarse para descomponer una señal arbitraria x(n) en una suma de unidades ponderadas y desplazadas muestras de la siguiente manera:

Esta descomposición se puede escribir de manera concisa como

donde cada término en la suma, x(k)S(n-k), es una señal que tiene una amplitud de x(k) en el tiempo n = k y un valor de ceropara todos los demás valores de n. Esta descomposición es la versión discreta de la propiedad svting para tiempo continuo señales y se utiliza en la derivación de la suma de convolución.

1.3 Sistemas de tiempo discreto 

 Un sistema de tiempo discreto es un operador matemático o mapeo que transforma una señal (la entrada) en otra señal (la salida) por medio de un conjunto fijo de reglas u operaciones. La notación T[-] se usa para representar un general como se muestra en la figura 1-4, en el que una señal de entrada x(n) se transforma en una señal de salida y(n) a través de la transformación T[.]. Las propiedades de entrada-salida de un sistema se pueden especificar en cualquiera de una serie de diferentes caminos. La relación entre la entrada y la salida, por ejemplo, puede expresarse en términos de un regla o función matemática concisa tal como

Sin embargo, también es posible describir un sistema en términos de un algoritmo que proporciona una secuencia de instrucciones. u operaciones que se van a aplicar a la señal de entrada, como

yl(n) = 0,5 yil(n - 1) +0,25x(n)

y2(n) = 0,25y2(n - 1) +0,5x(n)

ys(n) = 0.4y3(n - 1) +0.5x(n)

y(n) = YI(~) +y2(n) +ydn)

En algunos casos, un sistema puede especificarse convenientemente en términos de una tabla que define el conjunto de todos los posibles pares de señales de entrada-salida de interés

Figura 1-4. La representación de un sistema de tiempo discreto como una transformación T[.] que mapea una señal de entrada x(n) en una salida señal y(n).

Los sistemas de tiempo discreto pueden clasificarse en términos de las propiedades que poseen. Los más comunes las propiedades de interés incluyen linealidad, cambio de invariancia, causalidad, estabilidad e invertibilidad. Estas propiedades, junto con algunos otros, se describen en la siguiente sección.

1.3.1 Propiedades de los sistemas 

 Sistema sin memoria

La primera propiedad se refiere a si un sistema tiene o no memoria.

Definición: Se dice que un sistema no tiene memoria si la salida en cualquier momento x(n) = y(n) depende solo en la entrada en el tiempo n = no.

En otras palabras, un sistema no tiene memoria si, para cualquier no, podemos determinar el valor de y(no) dado solo el valor de x(no).

EJEMPLO 1.3.1 El sistema y(n) = x2b no tiene memoria porque y(no) depende solo del valor de x(n) en el tiempo no.

 El sistema y(n) = x(n) + x(n -I) por otro lado, no carece de memoria porque la salida en el tiempo no depende del valor de la entrada tanto en el tiempo no como en el tiempo no - 1.

Aditividad

Un sistema aditivo es aquel en el que la respuesta a una suma de entradas es igual a la suma de las entradas individualmente. De este modo,

Definición: Se dice que un sistema es aditivo si

T[xl(n)+ x2(n)I = T[x~(n)l+ T[x2(n)l

para cualquier señal XI (n) y x2 (n).

Homogeneidad

Se dice que un sistema es homogéneo si escalar la entrada por una constante resulta en una escala de la salida por la  la misma cantidad. Específicamente,

Definición: Se dice que un sistema es homogéneo si

T [cx(n)] = cT [x(n)]

para cualquier constante compleja c y para cualquier secuencia de entrada x(n).

EJEMPLO 1.3.2 El sistema definido por y(n) = (x^2(n))/(x(n-1)) 

Este sistema es , sin embargo, homogéneo porque, para una entrada cx(n) la salida es

Por otro lado, el sistema definido por la ecuación

es aditivo porque

Este sistema es, sin embargo, homogéneo porque, para una entrada cx(n) la salida es

Por otro lado, el sistema definido por la ecuación

Sin embargo, este sistema no es homogéneo porque la respuesta a cx(n) es

T[cx(n)]= cx(n) + c*x*(n - 1)

que no es lo mismo que

cT[x(n)] = cx(n) +cx*(n - 1)

Sistemas Lineales

Se dice que un sistema que es tanto aditivo como homogéneo es lineal. De este modo,

Definición: Se dice que un sistema es lineal si

T[am(n)+am(n)l = alT[x~(n)l+azT[xAn)l

para dos entradas cualesquiera xl(n) y x2(n) y para cualesquiera constantes complejas a1 y a2.

La linealidad simplifica enormemente la evaluación de la respuesta de un sistema a una entrada dada. Por ejemplo, usando el descomposición para x(n) dada en la ecuación. (1.4), y usando la propiedad de aditividad, se sigue que la salida y(n) puede escribirse como

Como los coeficientes x(k) son constantes, podemos usar la propiedad de homogeneidad para escribir

Si definimos hk(n) como la respuesta del sistema a una muestra unitaria en el tiempo n = k,

ecuación (1.5) se convierte en

que se conoce como la suma de superposición.

Cambio-Invarianza

Si un sistema tiene la propiedad de que un cambio (retraso) en la entrada por no resulta en un cambio en la salida por no, el sistema se dice que es invariante por desplazamiento. Más formalmente,

Definición: Sea y(n) la respuesta de un sistema a una entrada arbitraria x(n). el sistema es dicho que es invariante con el desplazamiento si, para cualquier retraso no, la respuesta a x(n -no) es y(n -no). Un sistema que no es invariante por turnos se dice que es variable por turnos.~

En efecto, un sistema será invariante al cambio si sus propiedades o características no cambian con el tiempo. para probar cambio de invariancia uno necesita comparar y(n -no) con T[x(n-no)]. Si son iguales para cualquier entrada x(n) y para todos los turnos no, el sistema es invariable por turnos.

EJEMPLO 1.3.3 El sistema definido por y(n) = x2(n) es invariante al desplazamiento, lo que se puede mostrar de la siguiente manera. Si y(n) =x2(n)es la respuesta del sistema a x(n),la respuesta del sistema para x'(n) = x(n -no)

Como y'(n) = y(n -no), el sistema es invariante frente al desplazamiento. Sin embargo, el sistema descrito por la ecuación

mientras que la respuesta a x(n - 1) =S(n - 1) es

Debido a que esto no es lo mismo que y(n - 1) = 2S(n - I), el sistema varía por turnos

~algunos autores se refieren a esta propiedad como rime-invorionce.Sin embargo. porque n no representa necesariamente "tiempo:" la invariancia de desplazamiento es un poco mas general.

Sistemas lineales Shin-Invariante

Un sistema que es tanto lineal como invariante al cambio se denomina sistema lineal invariante al cambio (LSI). Si h(n) es la respuesta de un sistema LSI a la muestra unitaria 6(n), su respuesta a 6(n - k) será h(n - k). Por lo tanto, en la suma de superposición dada en la ecuación. (1.6),

hk(n)= h(n -k)

y se sigue que M

y(n) = C *(k)h(n-k)

La ecuación (1.9, que se conoce como la suma de convolución, se escribe como donde * 

indica el operador de convolución. La secuencia h(n), denominada respuesta de muestra unitaria, proporciona una caracterización completa de un sistema LSI. En otras palabras, la respuesta del sistema a cualquier entrada x(n) puede se encuentra una vez que se conoce h(n).

Causalidad

Una propiedad del sistema que es importante para las aplicaciones en tiempo real es la causalidad, que se define de la siguiente manera:

Definición: Se dice que un sistema es causal si, para cualquier no, la respuesta del sistema en el tiempo

no depende solo de la entrada hasta el momento n = no.

Para un sistema causal, los cambios en la salida no pueden preceder a los cambios en la entrada. Así, si xl (n) = x2(n) para n 5 no, yl(n) debe ser igual a y2(n)para n 5 no. Por lo tanto, los sistemas causales se denominan no anticipatorios. Un sistema LSI será causal si y solo si h(n) es igual a cero para n < 0.

EJEMPLO 1.3.4 El sistema descrito por la ecuación y (n)= x(n) +x(n - 1) es causal porque el valor de la salida en cualquier tiempo n = no depende solo de la entrada x(n) en el tiempo no y en el tiempo no -1. El sistema descrito por y(n) = x(n)+ x(n+ I), por otro lado, es no causal porque la salida en el tiempo n = no depende del valor de la entrada en el tiempo no + 1. 

Estabilidad

En muchas aplicaciones, es importante que un sistema tenga una respuesta, y(n), que esté limitada en amplitud siempre que la entrada está limitada. Un sistema con esta propiedad se dice que es estable en la entrada acotada-salida acotada (BIBO) sentido. Específicamente,

Definición: Se dice que un sistema es estable en el sentido de entrada acotada-salida acotada si, por

cualquier entrada que esté acotada, Ix(n)l IA < m, la salida estará acotada,

Para un sistema lineal invariante por desplazamiento, la estabilidad está garantizada si la respuesta de la muestra unitaria es absolutamente sumable:

EJEMPLO 1.3.5 Un sistema LSI con respuesta de muestra unitaria h(n) = anu(n) será estable siempre que la1 < 1, porque

El sistema descrito por la ecuación y(n) = nx(n), por otro lado, no es estable porque la respuesta a un escalón unitario,x(n)= u(n), es y(n) = nu(n), que no tiene límites.

invertibilidad

Una propiedad del sistema que es importante en aplicaciones como la ecualización de canales y la desconvolución es la invertibilidad. Se dice que un sistema es invertible si la entrada al sistema puede determinarse únicamente a partir de la salida. En orden  para que un sistema sea invertible, es necesario que entradas distintas produzcan salidas distintas. En otras palabras, dado cualquiera de las dos entradas xl(n) y xz(n) con xl(n)# xz(n), debe ser cierto que yl(n) # y2(n).

EJEMPLO 1.3.6 El sistema definido por y(n) =x(n)g(n) es invertible si y solo si g(n) # 0 para todo n. En particular, dado y(n) con g(n) distinto de cero para todo n, x(n) puede recuperarse de y(n) como sigue:

1.4 Convolución 11

 La relación entre la entrada a un sistema lineal invariante por desplazamiento, x(n), y la salida, y(n), viene dada por la suma de convolución 00 x(n)* h(n)= x(k)h(n-k) 

Dado que la convolución es fundamental para el análisis y la descripción de los sistemas LSI, en esta sección analizamos la Mecánica de realización de convoluciones. Comenzamos enumerando algunas propiedades de la convolución que pueden usarse para simplificar la evaluación de la suma de convolución.

1.4.1 Propiedades de convolución 

 La convolución es un operador lineal y, por lo tanto, tiene varias propiedades importantes, incluida la conmutativa, propiedades asociativas y distributivas. Las definiciones e interpretaciones de estas propiedades se resumen abajo.

Propiedad conmutativa

La propiedad conmutativa establece que el orden en que se convolucionan dos secuencias no es importante. Matemáticamente, la propiedad conmutativa es

Desde el punto de vista de un sistema, esta propiedad establece que un sistema con una respuesta de muestra unitaria h(n) y entrada x(n) se comporta exactamente de la misma manera que un sistema con respuesta muestral unitaria x(n) y una entrada h(n). Esto se ilustra en la figura 1-5(a).

Propiedad asociativa

El operador de convolución satisface la propiedad asociativa, que es

Desde el punto de vista de los sistemas, la propiedad asociativa establece que si dos sistemas con respuestas de muestra unitaria hl(n) y h2(n) están conectados en cascada como se muestra en la Fig. I-5(b), un sistema equivalente es aquel que tiene una unidad respuesta de muestra igual a la convolución de hl (n) y h2(n) 

 propiedad conmutativa

 propiedad asociativa

(c) La propiedad distributiva.

Figura 1-5. La interpretación de las propiedades de convolución desde el punto de vista de los sistemas.

Propiedad distributiva

La propiedad distributiva del operador de convolución establece que 

Desde el punto de vista de los sistemas, esta propiedad afirma que si dos sistemas con respuestas de muestra unitaria hl(n) y h2(n) están conectados en paralelo, como se ilustra en la figura 1-5(c), un sistema equivalente es aquel que tiene una muestra unitaria respuesta igual a la suma de h 1 (n) y h2(n):

1.4.2 Realización de circunvoluciones 

 Habiendo considerado algunas de las propiedades del operador de convolución, ahora veremos la mecánica de realizar circunvoluciones Hay varios enfoques diferentes que se pueden usar, y el que sea más fácil dependerá depende de la forma y el tipo de sucesiones que se van a convolucionar.

Evaluación Directa

Cuando las sucesiones que se están convolucionando pueden describirse mediante expresiones matemáticas simples de forma cerrada, la convolución a menudo se realiza más fácilmente evaluando directamente la suma dada en Eq. (I 7). Al realizar circunvoluciones directamente, generalmente es necesario evaluar sumas finitas o infinitas que involucran términos de la forma anor yaya. En la tabla 1-1 se enumeran expresiones de forma cerrada para algunas de las series más comunes.

EJEMPLO 1.4.1 Realicemos la convolución de las dos señales

y

Tabla 1-1 Expresiones de forma cerrada para algunas Serie Encontrados

Con la evaluación directa de la suma de convolución encontramos

Como u(k) es igual a cero para k < 0 y u(n -k) es igual a cero para k > n, cuando n < 0, no hay términos distintos de cero en la suma y y(n) = 0. Por otro lado, si n 3 0, 

Por lo tanto, 

 

Enfoque gráfico

Además del método directo, las circunvoluciones también se pueden realizar gráficamente. Los pasos involucrados en el uso el enfoque gráfico es el siguiente:

1. Trace ambas sucesiones, x(k) y h(k), como funciones de k.

2. Elija una de las secuencias, digamos h(k), e inviértala en el tiempo para formar la secuencia h(-k).

3. Cambia la secuencia invertida en el tiempo por n. [Nota: si n > 0, esto corresponde a un desplazamiento a la derecha (retraso), mientras que si n < 0, esto corresponde a un desplazamiento a la izquierda (avance).]

4. Multiplica las dos sucesiones x(k) y h(n - k) y suma el producto de todos los valores de k. La resultante valor será igual a y(n). Este proceso se repite para todos los turnos posibles, n.

EJEMPLO 1.4.2 Para ilustrar el enfoque gráfico de la convolución, evalúemos y(n) = x(n)*h(n) donde x(n) y h(n)

son las secuencias que se muestran en la Fig. 1-6 (a) y (b), respectivamente. Para realizar esta convolución, seguimos los pasos enumerados anteriormente:

1. Como x(k) y h(k) se grafican como una función de k en la figura 1-6 (a) y (b), a continuación elegimos una de las sucesiones

para invertir en el tiempo. En este ejemplo, invertimos el tiempo h(k), que se muestra en la figura 1-6(c).

2. Formando el producto, x(k)h(-k), y sumando k, encontramos que y(0) = 1.

3. Al desplazar h(k) a la derecha en uno, se obtiene la secuencia h(l - k) que se muestra en la figura 1-6(d). Formando el producto,

x(k)h(l - k), y sumando k, encontramos que y(1) = 3.

4. Al desplazar h(l - k) a la derecha, nuevamente se obtiene la secuencia h(2 - k) que se muestra en la figura 1-6(e). Formando el producto, x(k)h(2 -k), y sumando k, encontramos que y(2) = 6.

5. Continuando de esta manera, encontramos que y(3) = 5. y(4) = 3, y y(n) = 0 para n > 4.

6. A continuación, tomamos h(-k) y lo desplazamos a la izquierda en uno, como se muestra en la figura 1-6 (f). Como el producto, x(k)h(- 1 -k), es igual a cero para todo k, encontramos que y(- I) = 0. De hecho. y(n) = 0 para todo n < 0.

La figura 1-6 (g) muestra la convolución para todo n

Figura 1-6. El enfoque gráfico de la convolución.

Un hecho útil para recordar al realizar la convolución de dos secuencias de longitud finita es que si x(n) es de longitud L 1 y h(n) es de longitud L2, y(n) = x(n) * h(n) será de longitud 

Además, si los valores distintos de cero de x(n) están contenidos en el intervalo [ M,, N,] y los valores distintos de cero de h(n) son contenidos en el intervalo [Mh,Nh], los valores distintos de cero de y(n) estarán confinados al intervalo [M,+Mh, N, +Nh].

EJEMPLO 1.4.3 Considere la convolución de la secuencia 

1 Lon520 x(n) = 0 en caso contrario n-55n55 con h(n) = 0 en caso contrario 

Como x(n) es cero fuera del intervalo [lo, 201 y h(n) es cero fuera del intervalo [-5, 51, los valores distintos de cero de la convolución, y(n) = x(n) * h(n), estará contenida en el intervalo [5, 251.

Método de la regla de cálculo

Otro método para realizar circunvoluciones, que llamamos el método de la regla de cálculo, es particularmente conveniente cuando tanto x(n) como h(n) tienen una longitud finita y una duración corta. Los pasos involucrados en el método de la regla de cálculo son como sigue:

Escriba los valores de x(k) en la parte superior de una hoja de papel y los valores de h(-k) en la parte superior de otra hoja de papel como se ilustra en la figura 1-7.

Alinea los dos valores de secuencia x(0) y h(O), multiplica cada par de números y suma los productos a

formar el valor de y(0).

Deslice el papel con la secuencia invertida en el tiempo h(k)hacia la derecha por uno, multiplique cada par de números, sume los productos para encontrar el valor y(l), y repita para todos los desplazamientos a la derecha por n > 0. Haga lo mismo, desplazando la secuencia invertida en el tiempo hacia la izquierda, para encontrar los valores de y(n) para n i0.

Figura 1-7. El enfoque de la regla de cálculo para la convolución.

En Capítulo. 2 veremos que otra forma de realizar convoluciones es usar la transformada de Fourier.

1.5 Ecuaciones en diferencias 

 La suma de convolución expresa la salida de un sistema lineal invariante por desplazamiento en términos de una combinación lineal de los valores de entrada x(n). Por ejemplo, un sistema que tiene una respuesta de muestra unitaria h(n) = anu(n) se describe mediante la ecuación

Aunque esta ecuación permite calcular la salida y(n) para una entrada arbitraria x(n), a partir de un cálculo punto de vista esta representación no es muy eficiente. En algunos casos, puede ser posible expresar de manera más eficiente la salida en términos de valores pasados de la salida además de los valores actuales y pasados de la entrada. El anterior sistema, por ejemplo, se puede describir de manera más concisa de la siguiente manera:

La ecuación (I.lo) es un caso especial de lo que se conoce como ecuación en diferencia lineal con coeficiente constante, o LCCDE. La forma general de un LCCDE es

donde los coeficientes a(k) y h(k) son constantes que definen el sistema. Si la ecuación en diferencias tiene uno o más términos a(k) distintos de cero, se dice que la ecuación en diferencias es recursiva. Por otro lado, si todos los coeficientes a(k) son iguales a cero, se dice que la ecuación en diferencias no es recursiva. Por lo tanto, la ecuación. ( 1.lo) es un ejemplo de una ecuación de diferencia recursiva de primer orden, mientras que la ecuación. (1.9) es una no recursiva de orden infinito ecuación diferencial.

Las ecuaciones en diferencias proporcionan un método para calcular la respuesta de un sistema, y(n), a una entrada arbitraria

x(n). Sin embargo, antes de que estas ecuaciones puedan resolverse, es necesario especificar un conjunto de condiciones iniciales. Para ejemplo, con una entrada x(n) que comienza en el tiempo n = 0, la solución a la ecuación. (1.11) en el tiempo n = 0 depende de la valores de y(-l), . ..,y(-p). Por lo tanto, estas condiciones iniciales deben especificarse antes de la solución para n 2 0

Puede ser encontrado. Cuando estas condiciones iniciales son cero, se dice que el sistema está en reposo inicial. Para un sistema LSI que se describe mediante una ecuación en diferencias, la respuesta de la muestra unitaria, h(n), se encuentra mediante resolviendo la ecuación en diferencias para x(n) = 6(n)suponiendo reposo inicial. Para un sistema no recursivo, a(k) = 0, la la ecuación de diferencia se convierte en 

y la salida es simplemente una suma ponderada de los valores de entrada actuales y pasados. Como resultado, la respuesta de la muestra unitaria es simple

Por lo tanto, h(n) tiene una longitud finita y el sistema se denomina sistema de respuesta de impulso de longitud finita (FIR).

Sin embargo, si a(k) # 0, la respuesta de la muestra unitaria es, en general, de longitud infinita y el sistema se denomina

un sistema de respuesta de impulso de longitud infinita (IIR). Por ejemplo, si

la respuesta de la muestra unitaria es h(n) =anu(n).

Hay varios métodos diferentes que se pueden usar para resolver LCCDE para una entrada general x(n). La primera

es simplemente configurar una tabla de valores de entrada y salida y evaluar la ecuación de diferencia para cada valor de n.

Este enfoque sería apropiado si solo se necesita determinar algunos valores de salida. Otro enfoque es

para usar transformadas z. Este enfoque será discutido en el Cap. 4. El tercero es el enfoque clásico de encontrar

las soluciones homogéneas y particulares, que ahora describimos.

Dado un LCCDE, la solución general es una suma de dos partes,

donde yh(n) se conoce como solución homogénea e yp(n) es la solución particular. lo homogéneo

solución es la respuesta del sistema a las condiciones iniciales, suponiendo que la entrada x(n) =0. Lo particular

la solución es la respuesta del sistema a la entrada x(n), asumiendo condiciones iniciales cero.

La solución homogénea se encuentra resolviendo la ecuación en diferencias homogénea 

 

La solución a la Ec. (1.13) se puede encontrar suponiendo una solución de la forma

Sustituyendo esta solución en la Ec. (1.13)obtenemos la ecuación polinomial

o  

El polinomio entre llaves se llama polinomio característico. Como es de grado p, tendrá p raíces,que puede ser real o complejo. Si los coeficientes a(k) tienen valores reales, estas raíces se presentarán en pares complejos conjugados (es decir, por cada raíz compleja z, habrá otra igual a zf). Si las p raíces zi son distintas, zi # zk fork # i, la solución general de la ecuación en diferencias homogénea es 

donde las constantes Ak se eligen para satisfacer las condiciones iniciales. Para raíces repetidas, la solución debe modificarse de la siguiente manera. Si z I es una raíz de multiplicidad m con las raíces p -m restantes distintas, la solución homogénea se convierte en 

Para la solución particular, es necesario encontrar la sucesión yp(n) que satisfaga la ecuación en diferencia para el x(n) dado. En general, esto requiere algo de creatividad y perspicacia. Sin embargo, para muchas de las entradas típicas que nos interesa, la solución tendrá la misma forma que la entrada. 

La tabla 1-2 enumera la solución particular para algunas entradas comúnmente encontradas. Por ejemplo, si x(n) = anu(n), la solución particular será de la forma

siempre que a no sea una raíz de la ecuación característica. La constante C se encuentra sustituyendo la solución en la ecuación diferencia. Note que para x(n) = CS(n) la solución particular es cero. Como x(n) = 0 para n > 0, la muestra unitaria solo afecta la condición inicial de y(n).

Tabla 1-2 La solución particular a un LCCDE para varias entradas diferentes

EJEMPLO 1.5.1 Encontremos la solución de la ecuación en diferencias y(n) -0.25y(n -2) =x(n)

para x(n) = u(n) suponiendo condiciones iniciales de y(- 1) = 1 y y(-2) = 0.

Comenzamos por encontrar la solución particular. De la Tabla 1-2 vemos que para x(n) = u(n)

y,(n) = CI

Sustituyendo esta solución en la ecuación en diferencias encontramos

IC -0.25IC = 1

Para que esto se mantenga, debemos tener

Para encontrar la solución homogénea, establecemos yh(n) = zn, lo que da el polinomio característico

z2 - 0,25 = 0

La solucion total 

Ahora se deben encontrar las constantes A, y A2 para que la solución total satisfaga las condiciones iniciales dadas, y(-1) = 1 y y(-2) = 0. Debido a que la solución dada en Eq. (1.17) solo se aplica para n 0, debemos derivar un conjunto equivalente de valores iniciales condiciones para y(0) e y(1). Evaluación de la ecuación. (1.16) en n = 0 y n = 1. tenemos 

 Sustituyendo estas condiciones iniciales derivadas en la ecuación. (1.17) tenemos

Resolviendo para A y A2 encontramos A, = -1/2 A2=-1/6 Por lo tanto, la solución es 

Aunque hasta ahora nos hemos centrado en ecuaciones en diferencias lineales con coeficientes constantes, no todos los sistemas y no todas las ecuaciones en diferencias de interés son lineales, y no todas tienen coeficientes constantes. un sistema que calcula un promedio móvil de una señal x(n) en el intervalo [0, n], por ejemplo, está definido por 

 Este sistema se puede representar mediante una ecuación en diferencias que tiene un coeficiente variable en el tiempo 

Aunque más complicadas y difíciles de resolver, las ecuaciones en diferencias no lineales o ecuaciones en diferencias con los coeficientes variables en el tiempo son importantes y surgen con frecuencia en muchas aplicaciones

Problemas Resueltos 

 Determine si las siguientes señales son periódicas o no y, para cada señal que sea periódica, determine

período fundamental 

Porque 0.125~ = n/8, y

cos (f n) = cos (I (n + 16))

x(n) es periódica con periodo N = 16

B) Aquí tenemos la suma de dos señales periódicas,

siendo el periodo de la primera señal igual a Nl = 24, y el periodo de la segunda, N2 = 36. Por lo tanto,

el periodo de la suma es 

N= N1N2 - (24)(36) -(24)(36) - 72 - mcd(N1, N2) mcd(24,36) 12

c) Para que esta secuencia sea periódica, debemos poder encontrar un valor para N tal que sin@ + 0.h) = sin(a  +0.2 (n + N)) La función seno es periódica con un período de 2~. Por lo tanto, 0.2N debe ser un múltiplo entero de 271. Sin embargo, como H es un número irracional, no existe ningún valor entero de N que haga verdadera la igualdad. Por lo tanto, este La secuencia es aperiódica.

d) Aquí tenemos el producto de dos sucesiones periódicas con periodos NI =32 y N2 =34. Por lo tanto, el verod fundamental es 

1.2 Encuentre las partes pares e impares de las siguientes señales: 

La parte par de una señal x(n) viene dada por

x,(n) = f [x(n)+x(-n)l

Con x(n) = u(n), tenemos 

que puede escribirse de manera concisa como

x,(n) = f + fS(n)

que puede escribirse de manera concisa como 

 Por lo tanto, la parte par del escalón unitario es una sucesión que tiene un valor constante de 4 para todo n excepto en n = 0, donde

tiene un valor de 1.

La parte impar de una señal x(n) viene dada por la diferencia

xo(n) = i[x(n)-x(-n)] 

Con x(n) = u(n), esto se convierte en  

 donde sgn(n) es la función signum.

Con x(n) = anu(n), la parte par es

 

La parte extraña, por otro lado, es 

1.3 Si XI (n) es par y x2(n) es impar, ¿cuál es y(n) = xl (n) .x2(n)?

Si y(n) =xdn). xddn),

y(-n) =XI(-n) .xz(-n)

Como x, (n) es par, xl(n) =xl(-n), y como xz(n) es impar, x2(n) = -xz(-n). Por lo tanto, 

y se sigue que y(n) es impar.

1.4 Si x(n) = 0 para n < 0, obtenga una expresión para x(n) en términos de su parte par, xe(n), y, usando esta

expresión, encuentre x(n) cuando xe(n) = (0.9)lnlu(n). Determinar si es posible o no obtener una

expresión similar para x(n) en términos de su parte impar.

Porque

xdn) = f [x(n)+ x(-n)l

y x,(n) = i[x(n)-x(-n)]

tenga en cuenta que cuando x(n) = 0 para n -= 0,

xe(n) = ix(n) n > 0

y xe(n)= x(n) n = 0

Por lo tanto, x(n) se puede recuperar de su parte par de la siguiente manera:

Por ejemplo, con xe(n) = (0.9)lnlu(n), tenemos

A diferencia del caso en que solo se conoce la parte par de una secuencia, si solo se da la parte impar, no es posible

recuperar x(n). El problema está en recuperar el valor de x(0). Como x,(O) siempre es igual a cero, no hay

información en la parte impar de x(n) sobre el valor de x(0). Sin embargo, si nos dieran x(0) junto con la parte impar,

entonces, x(n) podría recuperarse para todo n.

1.5 Si xe(n) es la parte simétrica conjugada de una sucesión x(n), ¿qué simetrías tienen la secuencia real y la imaginaria?

partes de xe(n) poseen?

La parte simétrica conjugada de x(n) es

x&) = $[x(n)+ x*(-n)]

Expresando x(n) en términos de sus partes real e imaginaria, tenemos

Por lo tanto, la parte real de x,(n) es par y la parte imaginaria es impar.

1.6 Encuentra la parte simétrica conjugada de la secuencia

je jnn/4 x(n) =

La parte simétrica conjugada de x(n) es

xe(n)= i[x(n)+ x*(-n)] = 2 [J'ejn"/4-jejnnI4]= 0

Por lo tanto, esta secuencia es antisimétrica conjugada.

1.7 Dada la secuencia x(n) = (6 -n)[u(n)- u(n -6)], haga un bosquejo de

(4 yl(n)=x(4-n) (h) y2(n) = x(2n - 3)

(c) ydn) = x(8 -3n) (d) ydn) = x(n2 - 2n + 1)

CAP. 11 SEÑALES Y SISTEMAS 2 1

(a) La secuencia x(n), ilustrada en la figura 1-8(a), es una secuencia linealmente decreciente que comienza en el índice n = 0 y

termina en el índice n = 5. La primera sucesión que se dibujará, yl(n) = x(4 -n), se encuentra desplazando x(n) por

cuatro y con inversión del tiempo. Observe que en el índice n = 4, yl(n) es igual a x(0). Por lo tanto, yl(n) tiene un valor de 6

en n = 4 y decrece linealmente hacia la izquierda (valores decrecientes de n) hasta n = -1, más allá de lo cual y (n) = 0. El

la secuencia y(n) se muestra en la figura 1-8(b).

Figura 1-8. Realización de manipulaciones de señales.

(b) La segunda secuencia, y2(n) = x(2n - 3), se forma a través de la combinación de cambio de tiempo y reducción de muestreo. Por lo tanto, y&~) se puede graficar primero desplazando x(n) a la derecha por tres (retraso) como se muestra en

SEÑALES Y SISTEMAS [CAP. 1

Figura 1-8(c). Luego, la secuencia y2(n) se forma reduciendo el muestreo por un factor de 2 (es decir, manteniendo solo los números pares).

términos de índice como lo indican los círculos sólidos en la figura 1-8(c)). En la figura I-8(d) se muestra un esquema de yn(n).

(c) La tercera secuencia, y3(n) = x(8 -3n), se forma a través de una combinación de cambio de tiempo, reducción de muestreo y

inversión del tiempo. Para dibujar y3(n) comenzamos trazando x(8 - n), que se forma desplazando x(n) a la izquierda por

ocho (avance) y retrocediendo en el tiempo como se muestra en la Fig. 1-8(e). Entonces, y3(n) se encuentra extrayendo cada tercer

muestra de x(8 -n), como lo indican los círculos sólidos, que se representa en la figura 1-8(f).

(4 Finalmente, y4(n) = x(n2 - 2n + 1) está formado por una transformación no lineal de la variable de tiempo n. Esta secuencia

puede esbozarse fácilmente enumerando cómo se mapea el índice n. Primero, tenga en cuenta que si n 2 4 o n 5 -2, entonces

n2 -2n + 1 2 9 y, por lo tanto, y4(n) = 0. Para -I 5 n 5 3 tenemos

La secuencia y4(n) se dibuja en la figura 1-8(g).

1.8 La notación ~((n))~ se utiliza para definir la secuencia que se forma de la siguiente manera:

~((n))~ = x(n módulo N)

donde (n módulo N) es el entero positivo en el rango [0,N - 11 que queda después de dividir n por N.

Por ejemplo, ((3))g = 3, ((12))g = 4 y ((-6))d = 2. Si x(n) = (i)%in(nn/2)u( n), hacer un bosquejo de

(a)x((n))3 y (b)x((n -2))3.

(a) Comenzamos por notar que ((n))3, para cualquier valor de n, es siempre un número entero en el rango [O, 21. De hecho, porque

((n))3 = ((n + 3k)h para cualquier k,

Por lo tanto, x((n))3 es periódico con un período N = 3. Por lo tanto, se sigue que ~((n))~ se forma repitiendo periódicamente

los primeros tres valores de x(n) como se ilustra en la siguiente figura:

(b) La secuencia x((n -2))3 también es periódica con un período N = 3, excepto que la señal se desplaza a la derecha por

no = 2 en comparación con la secuencia periódica de la parte (a). Esta secuencia se muestra en la siguiente figura:

1.9 La potencia en una señal de valor real x(n) se define como la suma de los cuadrados de los valores de la secuencia:

Supongamos que una sucesión x(n) tiene una parte par x,(n) igual a

CAP. I] SEÑALES Y SISTEMAS 23

Si la potencia en x(n) es P = 5, encuentre la potencia en la parte impar, x,(n), de x(n).

Este problema requiere encontrar la relación entre la potencia en x(n) y la potencia en las partes pares e impares.

Por definición, x(n) = x,(n) + x,(n). Por lo tanto,

Note que x,(n)x,(n) es el producto de una secuencia par y una secuencia impar y, por lo tanto, el producto es impar.

Como la suma de todos los n de una sucesión impar es igual a cero,

Por tanto, la potencia en x(n) es m m

que dice que la potencia en x(n) es igual a la suma de las potencias en sus partes pares e impares. Evaluando el poder

en el e incluso parte de x(n), encontramos

m m 2n PC = ):(ynl= -I +2 ):(f) = f n=-m n=O

Por tanto, con P = 5 tenemos 10 P,= 5 -P, = T

1.10 Considere la secuencia

Encuentre el valor numérico de

Calcule la potencia en x(n), W

Si x(n) es entrada a un sistema variable en el tiempo definido por y(n)

señal (es decir, evaluar la suma)

Esta es una aplicación directa de la serie geométrica.

Con la sustitución de -n por n tenemos

Por lo tanto, de la serie geométrica se sigue que

= nx(n), encuentre la potencia en la salida

SEÑALES Y SISTEMAS [CAP. 1

(h) Para encontrar la potencia en x(n) debemos evaluar la suma

Reemplazando n por -n y usando la serie geométrica, esta suma se convierte en

(c) Finalmente, para encontrar la potencia en y(n) = nx(n) debemos evaluar la suma

En la Tabla 1-I hay una expresión de forma cerrada para la suma

pero no para C:,n2an. Sin embargo, podemos derivar una expresión de forma cerrada para esta suma como sigue^.^ Diferenciando ambos lados de la ecuación. (1.19) con respecto a a, tenemos

Por lo tanto. tenemos la suma

Usando esta expresión para evaluar la Ec. (1.18). encontramos

1.11 Expresar la sucesión

Yo 1 n=O

2 n=l .r(n) = 3 n=2

0 más

como una suma de pasos unitarios escalados y desplazados.

En este problema, nos gustaría realizar una descomposición de señales, expresando x(n) como una suma de escalado y desplazado

pasos de la unidad. Hay varias formas de derivar esta descomposición. Una forma es expresar x(n) como una suma de

y muestras unitarias desplazadas,

x(n) = S(n)+ 2S(n - I) + 3S(n -2)

y use el hecho de que una muestra unitaria se puede escribir como la diferencia de dos pasos de la siguiente manera:

Por tanto, x(n)= u(n)- u(n -I) + 2[u(n-I) - u(n -2)] + 3[u(n-2) - u(n - 3)]

lo que da la descomposición deseada:

"su método es muy útil y debe ser recordado

CAP. I] SEÑALES Y SISTEMAS 25

Otra forma de derivar esta descomposición más directamente es la siguiente. En primer lugar, observamos que la descomposición debe

comenzar con un paso unitario, que genera un valor de I en el índice n = 0. Debido a que x(n) aumenta a un valor de 2 en n = 1,

debemos agregar un escalón unitario retrasado u(n - 1). En n = 2, x(n) nuevamente aumenta en amplitud en 1, por lo que agregamos el retraso

escalón unitario u(n -2). En este punto, tenemos

Por lo tanto, todo lo que queda es volver a llevar la secuencia a cero para n > 3. Esto se puede hacer restando el retardo

paso unitario 3u(n - 3), que produce la misma descomposición que antes.

Sistemas de tiempo discreto

1.12 Para cada uno de los siguientes sistemas, x(n) es la entrada e y(n) es la salida. Determinar qué sistemas son

homogéneos, qué sistemas son aditivos y cuáles son lineales.

(a) Si el sistema es homogéneo,

y(n) = T[cx(n)] = cT[x(n)]

para cualquier entrada x(n) y para todas las constantes complejas c. El sistema y(n) = log(x(n)) no es homogéneo porque

la respuesta del sistema a xl(n) = cx(n) es

que no es igual a c log(x(n)). Para que el sistema sea aditivo, si yl(n) e y2(n) son las respuestas a las entradas

y xz(n), respectivamente, la respuesta a x(n) = xl(n) + x2(n) debe ser y(n) = yl(n) + y2(n). Para esto

sistema que tenemos

T[xl(n) +xhN = log[x~(n)+x2(n)l # log[x~(n)l+ log[x2(n)l

Por lo tanto, el sistema no es aditivo. Finalmente, debido a que el sistema no es ni aditivo ni homogéneo, el

sistema es no lineal.

(b) Tenga en cuenta que si y(n) es la respuesta a x(n).

la respuesta a xl(n) = cx(n) es

que no es lo mismo que y1 (n). Por lo tanto, este sistema no es homogéneo. Del mismo modo, tenga en cuenta que la respuesta a

x(n) = x,(n) +x2(n) es

que no es igual a yl(n) +y2(n). Por lo tanto, este sistema no es aditivo y, como resultado, no es lineal.

SEÑALES Y SISTEMAS [CAP. 1

Este sistema es homogéneo, porque la respuesta del sistema a xl(n) = cx(n) es

El sistema es claramente, sin embargo, no aditivo y por lo tanto no lineal.

Sean y,(n) e yz(n) las respuestas del sistema a las entradas x,(n) y x2(n), respectivamente. la respuesta a

la entrada

x(n) = axl(n) + bxz(n)

y(n) = x(n) sen (y ) = [axl (n) + bx2(n)] sen r;-

1

Por tanto, se deduce que este sistema es lineal y, por tanto, aditivo y homogéneo.

Como la parte real de la suma de dos números es la suma de las partes reales, si y,(n) es la respuesta de la

sistema toxl(n), y yz(n) es la respuesta a x2(n), la respuesta a y(n) = yl(n) + yz(n) es

Por lo tanto el sistema es aditivo. Sin embargo, no es homogéneo porque

a menos que c sea real. Por lo tanto, este sistema es no lineal.

Para una entrada x(n), este sistema produce una salida que es la parte simétrica conjugada de x(n). Si c es un complejo

constante, y si la entrada al sistema es xl(n) = cx(n), la salida es

Por lo tanto, este sistema no es homogéneo. Este sistema es, sin embargo, aditivo porque

1.13 Un sistema lineal es homogéneo y aditivo.

(a) Dé un ejemplo de un sistema que sea homogéneo pero no aditivo.

(b) Dé un ejemplo de un sistema que sea aditivo pero no homogéneo.

Hay muchos sistemas diferentes que son homogéneos o aditivos, pero no ambos. Un ejemplo de un sistema

homogéneo pero no aditivo es el siguiente:

x(n -I)x(n) ~(n)= x(n + I)

Específicamente, tenga en cuenta que si x(n) se multiplica por una constante compleja c, la salida será

cx(n-l)cx(n) x(n-I)x(n) ~(n)= = c cx(n+ yo) x (n + 1)

que es c veces la respuesta a x(n). Por lo tanto, el sistema es homogéneo. Por otro lado, debe quedar claro

que el sistema no es aditivo porque, en general,

{xl(n - 1) + XZ(~ -l)J(x~(n)+xz(n)I x~(n-l)x~(n)+ xdn -l)xz(n)

x~(n+ 1) +xAn + I) + x,(n + 1) xz(n + 1)

CAP. I] SEÑALES Y SISTEMAS

Un ejemplo de un sistema que es aditivo pero no homogéneo es

La aditividad se deriva del hecho de que la parte imaginaria de una suma de números complejos es igual a la suma de números imaginarios

partes. Este sistema no es homogéneo, sin embargo, porque

1.14 Determine si cada uno de los siguientes sistemas es o no invariante frente al desplazamiento:

(a) Sea y(n) la respuesta del sistema a una entrada arbitraria x(n). Para probar la invariancia de cambio, queremos comparar

la respuesta desplazada y(n -no) con la respuesta del sistema a la entrada desplazada .r(n -nu). Con

tenemos. para la respuesta desplazada.

Ahora, la respuesta del sistema a xl(n) = x(n -no) es

Como yl(n)= y(n - no), el sistema es invariante tras desplazamientos.

(6) Este sistema es un caso especial de un sistema más general que tiene una descripción de entrada-salida dada por

donde f (n) es una ganancia variable por desplazamiento. Los sistemas de esta forma siempre varían por turnos siempre que f (n) no sea una constante.

Para mostrar esto, suponga que f(n) no es constante y sean nI y nz dos índices para los cuales f (n,) # f (nz). Con

una entrada .rl(n)= S(n -nl), tenga en cuenta que la salida yl(n) es

Si, por el contrario, la entrada es x2(n) = 6(n -n2), la respuesta es

Aunque .t.,(n) y xZ(n) difieren solo en un desplazamiento, las respuestas yl(n) e y2(n) difieren en un desplazamiento y un cambio en

amplitud. 'Por lo tanto, el sistema varía por turnos.

(c) Deja

sea la respuesta del sistema a un impulso arbitrario .r(n). La respuesta del sistema a la entrada desplazada.

.rl(n) = x(n - no) es

Debido a que esto es igual a v(n - no), el sistema es invariante frente al desplazamiento.

SEÑALES Y SISTEMAS [CAP. 1

(d) Este sistema varía por turnos, lo que se puede mostrar con un simple contraejemplo. Tenga en cuenta que si x(n) = S(n), la

la respuesta será y(n) = 6(n). Sin embargo, sixl(n) = 6(n-2). la respuesta será yl(n) =xl(n2)= 6(n2-2) = 0,

que no es igual a y(n - 2). Por lo tanto, el sistema es variable por turnos.

(e) Con y(n) la respuesta a x(n), observe que para la entrada xl(n)= x(n -N), la salida es

que es lo mismo que la respuesta tox(n). Debido a que yl (n) # y(n- N), en general, este sistema no es invariante por corrimiento.

(f) Se puede demostrar fácilmente que este sistema varía por turnos con un contraejemplo. Sin embargo, supongamos que usamos el

enfoque directo y sea x(n) una entrada y y(n) = x(-n) la respuesta. Si consideramos la entrada desplazada,

xl (n) =x(n - no), encontramos que la respuesta es

Sin embargo, tenga en cuenta que si cambiamos y(n) por no,

que no es igual a yl (n). Por lo tanto, el sistema es variable por turnos.

1.15 Un sistema lineal de tiempo discreto se caracteriza por su respuesta hk(n) a una muestra unitaria retardada S(n - k).

Para cada sistema lineal definido a continuación, determine si el sistema es o no invariante al desplazamiento.

(a) hk(n) = (n -k)u(n -k)

(6) hk(n) = S(2n -k)

S(n -k - 1) k par

5u(n -k) k impar

(a) Note que hk(n)es una función de n - k. Esto sugiere que el sistema es invariante al cambio. Para verificar esto, sea y(n)

Sea la respuesta del sistema a x(n):

La respuesta a una entrada desplazada, x(n - no), es

Con la sustitución 1 = k -no esto se convierte en

De la expresión para y(n) dada en la Eq. (1.24, vemos que

que es lo mismo que yl(n). Por lo tanto, este sistema es invariante por desplazamiento.

CAP. I] SEÑALES Y SISTEMAS 29

(h) Para el segundo sistema, hI(n) no es una función de n - k. Por lo tanto, debemos esperar que este sistema varíe por turnos. Veamos si podemos encontrar un ejemplo que demuestre que es un sistema variable por turnos. para la entrada

~(11)= 6(11), la respuesta es

Debido a que gl(n) # y(n - I ), el sistema varía por turnos.

(c) Finalmente, para el último sistema, vemos que aunque hk(n) es una función de n -k par par y una función de (n -k)

tenedor extraño,

11k(n)# hk-~(n-1)

En otras palabras, la respuesta del sistema a 6(n -k - 1) no es igual a la respuesta del sistema a 6(n -k)

retrasado por 1. Por lo tanto. este sistema es variable por turnos.

1.16 Sea Tr.1 un sistema lineal, no necesariamente invariante por corrimiento, que tiene una respuesta hk(n)a la entrada 6(n -k).

Derivar una prueba en términos de kk(n) que permita determinar si el sistema es estable o no y si

o no el sistema es causal.

(a) La respuesta de un sistema lineal a una entrada ~(n) es

Por lo tanto. la salida puede ser acosada de la siguiente manera:

Si x(n) está acotado, Ix(n)l 5 A < W,

lywi i A 2 IM~)I

Como resultado. si

la salida será limitada y el sistema es estable. La ecuación (1.23) es una condición necesaria para la estabilidad.

Para establecer la suficiencia de esta condición, mostraremos que si esta sumatoria no es finita, podemos encontrar un

entrada limitada que producirá una salida ilimitada. Supongamos que hk(n) está acotado para todo k y n

[De lo contrario, el sistema será inestable. porque la respuesta a la entrada acotada S(n -k) será ilimitada].

Con hi(tl) acotado para todo k y n, suponga que la suma en la Ec. (1.23) no está acotada para algún n, decir n = no.

Dejar

x(n) = signo(h,(n~)l

eso es,

Para esta Entrada, la respuesta en el tiempo n = no es

que, por suposición, es ilimitado. Por lo tanto, el sistema es inestable y hemos establecido la suficiencia

de la condición dada en la Ec. (1.23).

SEÑALES Y SISTEMAS [CAP. 1

(b) Consideremos ahora la causalidad. Para una entrada x(n), la respuesta es la dada en la ecuación. (1.22). Para un sistema

para ser causal, la salida y(n) en el momento no no puede depender de la entrada x(n) para cualquier n > no. Por lo tanto, la ecuación. (1.22)

debe ser de la forma

,I

y(n) = xhk(n)x(k)

k=-m

Esto, sin embargo, será cierto para cualquier x(n) si y sólo si

que es la prueba deseada de causalidad.

Determine si los sistemas definidos en el Prob. 1 .I5 son (a) estables y (b) causales.

(a) Para el primer sistema, hk(n)= (n -k)u(n -k), tenga en cuenta que hk(n) crece linealmente con n. Por lo tanto, este sistema

no puede ser estable. Por ejemplo, tenga en cuenta que si x(n)=S(n), la salida será

que es ilimitado. Alternativamente, podemos usar la prueba derivada en el Prob. 1 .I6 para comprobar la estabilidad. Porque

este sistema es inestable. Por otro lado, debido a que h,(n) = 0 para n < k, este sistema es causal.

(b) Para el segundo sistema, hk(n)= S(2n - k), tenga en cuenta que hl(n) tiene, como mucho, un valor distinto de cero, y este valor distinto de cero

valor es igual a I. Por lo tanto,

para todo n, y el sistema es estable. Sin embargo, el sistema no es causal. Para mostrar esto, observe que si x(n) = &(n-2),

la respuesta es

y(n) = h2(n)= 6(2n -2) = &(n-I)

Debido a que el sistema produce una respuesta antes de que ocurra la entrada, no es causal.

(c) Para el último sistema, tenga en cuenta que

cm norte

= xSu(n -k) = 15 A=-- A=-.u

A añadir h impar

que es ilimitado. Por lo tanto, este sistema es inestable. Finalmente, debido a que hk(n)= 0 para n < k, el sistema es

causal.

Considere un sistema lineal que tiene una respuesta a un escalón unitario retrasado dada por

Es decir, sk(n) es la respuesta del sistema lineal a la entrada x(n) = u(n -k). Encuentre la respuesta de este

sistema a la entrada x(n) = 6(n - k), donde k es un entero arbitrario, y determinar si esto o no

sistema es invariante por desplazamiento, estable o causal.

Debido a que este sistema es lineal, podemos encontrar la respuesta, hk(n), a la entrada &(n-k) de la siguiente manera. Con &(n-k) =

u(n - k) -u(n -k -I), usando linealidad se sigue que

que se muestra a continuación:

CAP. 11 SEÑALES Y SISTEMAS

A partir de esta gráfica, vemos que el sistema no es invariante frente al desplazamiento, porque la respuesta del sistema a una muestra unitaria

cambios en la amplitud a medida que la muestra unitaria avanza o se retrasa. Sin embargo, debido a que hk(n)= 0 para n < k, el sistema

es causal. Finalmente, debido a que hk(n) no está acotado en función de k, se deduce que el sistema es inestable. En particular,

nótese que la prueba de estabilidad de un sistema lineal derivada del prob. 1.16 requiere que

Para este sistema,

Tenga en cuenta que al evaluar esta suma, estamos sumando sobre k. Esto se realiza más fácilmente trazando hk(n) frente a n

como se ilustra en la siguiente figura.

Debido a que esta suma no puede estar limitada por un número finito B, este sistema es inestable. Como este sistema es inestable,

deberíamos poder encontrar una entrada limitada que produzca una salida ilimitada. Una de esas secuencias es la siguiente:

la respuesta es

y(n) = n(-l)"u(n)

que es claramente ilimitado.

1.19 Considere un sistema cuya salida y(n) está relacionada con la entrada x(n) por

Determine si el sistema es o no (a) lineal, (b) invariante por desplazamiento, (c) estable, (d) causal.

SEÑALES Y SISTEMAS [CAP. I

(a) Lo primero que debemos observar acerca de y(n) es que se forma sumando productos de .r(n) con desplazamiento

versiones de sí mismo. por ejemplo Xi

y(O) = .r2(k)

yo=-w

Esperamos, por lo tanto, que este sistema sea no lineal. Confirmemos esto con un ejemplo. Tenga en cuenta que si .r(n) = 6(n),

y(n) = S(n). Sin embargo, si x(n) = 2S(n), y(n) = 46(n). Por lo tanto. el sistema no es homogéneo y,

en consecuencia, es no lineal.

(b) Para la invariancia de desplazamiento, queremos comparar

,-

y(n - no) = C x(k)x(n -no + k) I=-n;

a la respuesta del sistema a xl(n) = x(n -rill). cual es

donde la última igualdad sigue con la sustitución k' = k - ncl. Como y,(n) # y(n -nu), este sistema es

no cambia-invariante.

(c) Para la estabilidad, tenga en cuenta que si x(n) es un escalón unitario, y(0) no está acotado. Por lo tanto, este sistema es inestable.

(d) Finalmente, para la causalidad, observe que la salida depende de los valores de .t (11) para todo n. Por ejemplo, y(O) es la suma

de los cuadrados de x(k) para todo k. Por lo tanto, este sistema no es causal.

1.20 Dado que x(n) es la entrada del sistema y y(n) es la salida del sistema, ¿cuáles de los siguientes sistemas son

¿causal?

(d) y(n) = r(n) -x(n2 - n)

norte

(e) y(n) = nx(n - k)

(a) El sistema y(n) = r2(n)u(n) no tiene memoria (es decir, la respuesta del sistema en el instante n depende únicamente de la

entrada en el tiempo n y en ningún otro valor de la entrada). Por lo tanto, este sistema es causal.

(b) El sistema y(n) = x(ln1) es un ejemplo de un sistema no causal. Esto se puede ver mirando la salida cuando

n < 0. En particular, observe que y(- I) = s(l). Por lo tanto. la salida del sistema en el tiempo 11 = -1 depende de

el valor de la entrada en un tiempo futuro.

(c) Para este sistema, con el fin de calcular la salida ut y(n) en el tiempo n todo lo que necesitamos saber es el valor de la entrada x(n)

a veces n, n -3 y n - 10. Por lo tanto. este sistema debe ser causal.

(d) Este sistema no es causal, lo que puede verse evaluando v(n) para 11 < 0. Por ejemplo,

Como y(- I) depende del valor de .r(2), que ocurre después del tiempo n = -I, este sistema no es causal

CAP. 11 SEÑALES Y SISTEMAS 3 3

(e) La salida de este sistema en el tiempo n es el producto de los valores de la entrada x(n) en los tiempos n - 1, . . . , n-n

Por lo tanto, debido a que la salida depende solo de los valores pasados de la señal de entrada, el sistema es causal.

(f) Este sistema no es causal, lo que puede verse fácilmente si reescribimos la definición del sistema de la siguiente manera:

Por lo tanto, la entrada debe conocerse para todo n 5 0 para determinar la salida en el tiempo n. Por ejemplo, para encontrar y(-5)

debemos saber x(O), x(- I), x(-2), . . .. Por lo tanto, el sistema es no causal.

1.21 Determine cuáles de los siguientes sistemas son estables:

(b) y (n)= ex(")/x(n - 1)

(a) Sea x(n) cualquier entrada acotada con Ix(n)l c M . Entonces se deduce que la salida, y(n) = x2(n), puede estar acotada

por

I~(n)l= lx(n)12 < M2

Por lo tanto, este sistema es estable,

(b) Este sistema claramente no es estable. Por ejemplo, observe que la respuesta del sistema a una muestra unitaria x(n) = S(n)

es infinito para todos los valores de n excepto n = 1.

(c) Como Icos(x)l 5 1 para todo x, este sistema es estable.

(d) Este sistema corresponde a un integrador digital y es inestable. Considere, por ejemplo, la respuesta escalonada del

sistema. Con x(n) = u(n) tenemos, para n 2 0,

Aunque la entrada está acotada, (x(n)l 5 1), la respuesta del sistema no está acotada.

(e) Se puede demostrar que este sistema es estable usando la siguiente desigualdad:

Específicamente, si x(n) está acotado, Ix(n)l < M,

Por lo tanto, la salida está acotada y el sistema es estable.

(f) Este sistema no es estable. Esto puede verse considerando la entrada acotada x(n) = cos(nrr/l). Específicamente,

tenga en cuenta que la salida del sistema en el tiempo n = 0 es

que es ilimitado. Alternativamente, debido a que la relación entrada-salida es de convolución, esta es una relación lineal

sistema invariante de desplazamiento con una respuesta de muestra unitaria

h(n)= porque (7)

SEÑALES Y SISTEMAS [CAP. 1

Debido a que un sistema lineal invariante por corrimiento será estable solo si

vemos que este sistema no es estable.

1.22 Determine cuáles de los siguientes sistemas son invertibles:

Para probar la invertibilidad, podemos mostrar que un sistema es invertible diseñando un sistema inverso que se recupera únicamente

la entrada de la salida, o podemos mostrar que un sistema no es invertible encontrando dos entradas diferentes que producen

la misma salida. Cada sistema definido anteriormente se probará para la invertibilidad utilizando uno de estos dos métodos.

(a) Este sistema es claramente invertible porque, dada la salida y(n), podemos recuperar la entrada usando x(n) = 0.5y(n).

(h) Este sistema no es invertible, porque el valor de x(n) en 11 = 0 no se puede recuperar de y(n). Por ejemplo,

la respuesta del sistema a X(R) ya xl(n)=x(n)+a&n) será la misma para cualquier a.

(c) Debido a la diferenciación entre dos valores de entrada sucesivos, este sistema no será invertible. Por ejemplo,

tenga en cuenta que las entradas x(n) y x(n) + c producirán la misma salida para cualquier valor de c.

(6) Este sistema corresponde a un integrador y es un sistema invertible. Para demostrar que es invertible, podemos

construir el sistema inverso, que es

.u(n)= y(n) -y(n -I)

Para mostrar que este es el sistema inverso, tenga en cuenta que

n-l

(e) La invertibilidad debe ser válida tanto para señales complejas como para señales de valor real. Por lo tanto, este sistema es no invertible porque

descarta la parte imaginaria 01' x(n). Se podría afirmar, sin embargo, que este sistema es invertible sobre el conjunto de

señales de valor real.

1.23 Considere la cascada de dos sistemas. SI y S2.

(a) Si tanto SI como S2 son lineales, invariantes al desplazamiento, estables y causales, ¿la cascada también será lineal?

invariante al cambio, estable y causal?

(b) Si tanto SI como S2 son no lineales, ¿será no lineal la cascada?

(c) Si tanto SI como S2 varían según el turno, ¿la cascada variará según el turno?

(a) Se demuestra fácilmente que la linealidad, la invariancia por desplazamiento, la estabilidad y la causalidad se conservan en una cascada. Por ejemplo,

la respuesta de SI a la entrada nxl(n) +hxz(n)será awl(n)+bw2(n)debido a la linealidad de S,. Con esto como

la entrada a S2, la respuesta será, nuevamente por linealidad, ay,(n)+ hy7(n). Por lo tanto, si tanto S I como S2 son lineales,

la cascada será lineal.

CAP. 11 SEÑALES Y SISTEMAS 35

De manera similar, para la invariancia de desplazamiento, si se ingresa x(n -no) en S, la respuesta será w(n - no). Además,

debido a que S2 es invariante con el desplazamiento, la respuesta a w ( n - n o ) será y(n -no). Por lo tanto, la respuesta de la cascada

a x(n -no) es y(n - no), y la cascada es invariante al desplazamiento.

Para establecer la estabilidad, observe que siendo SI estable, si x(n) está acotado, la salida w(n) estará acotada.

Con w(n) como entrada acotada al sistema estable S2, la respuesta y(n) también estará acotada. Por lo tanto, la

cascada es estable.

Finalmente, la causalidad de la cascada sigue observando que si S2 es causal, y(n) en tiempo n = no depende solo

en w(n)para n 5 no. Siendo SI causal, w(n)para n 5 no dependerá solo de la entrada x(n) para n 5 no, y

se sigue que la cascada es causal.

(b) Si SI y S2 no son lineales, no es necesariamente cierto que la cascada será no lineal porque el segundo sistema

puede deshacer la no linealidad de la primera. Por ejemplo, con

aunque tanto SI como Sz no son lineales, la cascada es el sistema de identidad y, por lo tanto, es lineal.

(c) Como en (b), si SI y S2 varían según el turno, no es necesariamente cierto que la cascada será variable según el turno. Para

ejemplo. si el primer sistema es un modulador.

y el segundo es un demodulador,

y(n) = w(n). e-Inq

la cascada es invariante con el desplazamiento, aunque un modulador y un demodulador varían con el desplazamiento. Otro ejemplo

es cuando Sl es un muestreador ascendente

y S2 es un muestreador descendente

y(n) = w(2n)

En este caso, la cascada es invariante por desplazamiento y y(n) = x(n). Sin embargo, si se invierte el orden de los sistemas,

la cascada ya no será invariante por desplazamiento. Además, si un sistema lineal invariante de desplazamiento, como un retraso unitario, es

insertada entre el up-sampler y el down-sampler, la cascada de los tres sistemas será, en general,

cambio de turno.

Circunvolución

1.24 El primer valor distinto de cero de una secuencia de longitud finita x(n) ocurre en el índice n = -6 y tiene un valor x(-6) = 3,

y el último valor distinto de cero ocurre en el índice n = 24 y tiene un valor x(24) = -4. ¿Cuál es el índice de la

primer valor distinto de cero en la convolución

y(n) = x(n) * x(n)

y cual es su valor ¿Qué pasa con el último valor distinto de cero?

Debido a que estamos convolucionando dos secuencias de longitud finita, el índice del primer valor distinto de cero en la convolución es

igual a la suma de los índices de los primeros valores distintos de cero de las dos secuencias que se están convolucionando. En este caso,

el índice es n = -12, y el valor es

y(-12) = x2(-6) = 9

De manera similar, el índice del último valor distinto de cero está en n = 48 y el valor es

1.25 La convolución de dos secuencias de longitud finita será de longitud finita. ¿Es cierto que la convolución de

una secuencia de longitud finita con una secuencia de longitud infinita será infinita en longitud?

SEÑALES Y SISTEMAS [CAP. I

No es necesariamente cierto que la convolución de una secuencia de longitud infinita con una secuencia de longitud finita será

infinito en longitud. Puede ser cualquiera. Claramente, si x(n) = 6(n) y h(n) = (OS)"u(n), la convolución será una

secuencia de longitud infinita. Sin embargo, es posible que la secuencia de longitud finita elimine la cola de longitud infinita de

una secuencia de longitud infinita. Por ejemplo, tenga en cuenta que

Por lo tanto, la convolución de x(n) = 6(n) -fS(n -I) con h(n) = (OS)"u(n) será de longitud finita:

1.26 Encuentre la convolución de las dos secuencias de longitud finita:

En la siguiente figura se muestran las sucesiones x(k) y h(k).

Como h(n) es igual a cero fuera del intervalo [-3, 31, y x(n) es cero fuera del intervalo [l, 51, la convolución

y(n) =x(n) * h(n) es cero fuera del intervalo 1-2, 81.

Una forma de realizar la convolución es utilizar el método de la regla de cálculo. Enumerar x(k) y h(-k) en dos piezas

de papel, alineándolos en k = 0, tenemos la imagen como se muestra a continuación (la secuencia h(-k) está al frente).

Formando la suma de los productos x(k)h(-k), obtenemos el valor de y(n) en el tiempo n = 0, que es y(0) = 2. Desplazamiento

h(-k) a la izquierda por uno, multiplicando y sumando, obtenemos el valor de y(n) en n = -1, que es y(-I) = 2.

Desplazando una vez más a la izquierda, formando la suma de productos, encontramos y(-2) = 1, que es el último valor distinto de cero

de y(n) para n < 0. Repitiendo el proceso desplazando h(-k) hacia la derecha, obtenemos los valores de y(n) para n > 0,

cuales son

Otra forma de realizar la convolución es utilizar el hecho de que

x(n) * S(n -no) = x(n -no)

Escribiendo h(n) como

CAP. I] SEÑALES Y SISTEMAS

podemos evaluar y(n) de la siguiente manera

y(n) = 2x(n + 3) -2x(n + 1) + 2x(n - 1) - 2x(n - 3)

Hacer una tabla de estas secuencias desplazadas.

y sumando las columnas, obtenemos la sucesión y(n).

1.27 Deduzca una expresión de forma cerrada para la convolución de x(n) y h(n) donde

N-6

x(n) = (6) u(n)

h(n) = (f)"u(n-3)

Porque ambas secuencias tienen una longitud infinita. es más fácil evaluar la suma de convolución directamente:

Tenga en cuenta que debido a que x(n) = 0 para n < 0 y h(n) = 0 para n < 3, y(n) será igual a cero para n < 3. Sustituyendo

x(n) y h(n) en la suma de convolución, tenemos

Debido al paso u(k), el límite inferior de la suma puede cambiarse a k = 0, y debido a que u(n - k - 3) es cero para

k > n -3, el límite superior puede cambiarse a k = n - 3. Así. para n 2 3 la suma de convolución se convierte en

Usando la serie geométrica para evaluar la suma, tenemos

1.28 Un sistema lineal invariante por corrimiento tiene una respuesta de muestra unitaria

Encuentre la salida si la entrada es

x(n) = -n3"u(-n)

A continuación se muestran las secuencias x(n) y h(n).

38 SEÑALES Y SISTEMAS [CAP. I

Como x(n) es cero para n > -1, y h(n) es igual a cero para n > -1, la convolución será igual a cero para

n z -2. Evaluando la suma de convolución directamente, tenemos

Como u(-k) = 0 horquilla > 0 y u(-(n -k) - 1) = 0 horquilla < n + I, la cLa suma de onvolución se convierte en

Con el cambio de variables m = -k, y usando las fórmulas de series dadas en la Tabla I -I, tenemos

Revisemos esta respuesta para algunos valores de n usando convolución gráfica. Invirtiendo el tiempo x(k), vemos que h(k)

y x(-k) no se superponen para ningún k y, por lo tanto, y(0) = 0. De hecho, no es hasta que desplazamos x(-k) a la izquierda dos

que hay alguna superposición. Con x(-2 - k) y h(k) superpuestos en un punto, y siendo el producto igual a i,

se sigue que y(-2) = 4. Evaluando la expresión anterior para y(n) arriba en el índice n = -2, obtenemos el mismo

resultado. Para n = -3, las sucesiones x(-3 - k) y h(k) se superponen en dos puntos, y la suma de los productos da

y(-3) = f + $ = $, que, de nuevo, es lo mismo que la expresión anterior.

1.29 Si la respuesta de un sistema lineal invariante por corrimiento a un escalón unitario (es decir, la respuesta al escalón) es

encuentre la respuesta de la muestra unitaria, h(n).

En este problema, comenzamos observando que

S(n) = u(n)-u(n - 1)

Por lo tanto, la respuesta de la muestra unitaria, h(n), está relacionada con la respuesta al escalón, s(n), de la siguiente manera:

Así, dado s(n), tenemos

h(n) = s(n)-s(n-I)

= n(;)"u(n) -(n -I)(;) 11- 1

tu(n - yo)

= [.(;In -2(n - ~)(;)"]u(n-I)

= ( 2 -n)(i)"u(n-I)

1.30 Demostrar la propiedad conmutativa de la convolución

Demostrar la propiedad conmutativa es sencillo y solo implica una manipulación simple de la convolución.

suma. Con la convolución de x(n) con h(n) dada por

con la sustitución 1 = n -k, tenemos

y se establece la propiedad conmutativa.

CAP. 11 SEÑALES Y SISTEMAS

1.31 Demostrar la propiedad distributiva de la convolución

Para demostrar la propiedad distributiva, tenemos

Por lo tanto,

y se establece la propiedad.

1.32 Vamos

h(n) = 3(;)"u(n) - 2(;)"-'u(n)

sea la respuesta de la muestra unitaria de un sistema lineal invariante por desplazamiento. Si la entrada a este sistema es un escalón unitario,

1 onza

x(n) = 0 más

encuentre limn,, y(n) donde y(n) = h(n) * x(n).

Con M

y(n) = h(n)* x(n) = xh(k)x(n-k)

k=-w

si x(n) es un escalón unitario,

metro

Por lo tanto, lim y(n) = xh(k) n-cc k=-m

Evaluando la suma, tenemos

1.33 Convolución

con una rampa

La convolución de x(n) con h(n)es

metro

= z[(0.9)~u(k)][(n-k)u(n-k)]

k=-03

SEÑALES Y SISTEMAS [CAP. 1

Debido a que u(k) es horquilla cero < 0, y u(n -k) es horquilla cero > n, esta suma se puede reescribir de la siguiente manera:

Usando la serie dada en la Tabla 1-1, tenemos

que puede simplificarse a

y (n) = [Ion - 90 + 90(0.9)"]u(n)

1.34 Realizar la convolución

y(n)=x(n)* 0)

cuando h(n)= (;)"u(n)

y x(n)= (i)"[u(n)-u(n - 101)l

Con

comenzamos sustituyendo x(n) y h(n) en la suma de convolución

Para evaluar esta suma, que depende de n, consideramos tres casos. Primero, para n c 0, la suma es igual a cero porque

u(n - k) =0 para 0 5 k 5 100. Por lo tanto,

Segundo, observe que para 0 5 n 5 100, el paso u(n -k) es solo igual a 1 tenedor 5 n. Por lo tanto,

yo -(f) ,yo+l

= (f)" 1-1 = 3(;)"[1 -(f)"+']

CAP. 11 SEÑALES Y SISTEMAS

Finalmente, para n 2 100, observe que u(n -k) es igual a I para todo k en el rango 0 5 k 5 100. Por lo tanto,

1 - ($O'

=(f)" 1-2 = 3(!)"[l -(f)101] 3

En resumen, tenemos

1.35 Sea h(n) una exponencial truncada

y x(n) un pulso discreto de la forma

1 Osns5 x(n) =

0 más

Encuentre la convolución y(n) = h(n)* x(n).

Para encontrar la convolución de estas dos secuencias de longitud finita, necesitamos evaluar la suma

Para evaluar esta suma, será útil hacer un gráfico de h(k) y x(n -k) en función de k como se muestra en la siguiente

cifra:

Tenga en cuenta que la cantidad de superposición entre h(k) y x(n - k) depende del valor de n. Por ejemplo, si n < 0, hay

no hay superposición, mientras que para 0 5 n 5 5, las dos secuencias se superponen para 0 5 k 5 n. Por lo tanto, a continuación, nos

considere cinco casos separados.

Caso 1 n -= 0. Cuando n c 0, no hay superposición entre h(k) y x(n - k). Por lo tanto, el producto

h(k)x(n -k) = 0 para todo k, y y(n) = 0.

Caso 2 0 _< n 5 5. Para este caso, el producto h(k)x(n -k) es distinto de cero sólo para horquillas en el rango 0 5 k 5 n.

Por lo tanto,

SEÑALES Y SISTEMAS [CAP. 1

Caso 3 6 5 n 5 10. Para 6 5 n 5 10, todos los valores distintos de cero de x(n - k) están dentro de los límites de la

suma. y

Caso 4 1 I 5 n 5 15. Cuando n está en el rango I 1 5 n 5 15, las secuencias h(k) y x(n -k) se superponen para

n -5 5 k 5 10. Por lo tanto,

Caso 5 n > 15. Finalmente, para n > 15, nuevamente no hay superposición entre h(k) y x(n -k), y el producto

h(k)x(n -k) es igual a cero para todo k. Por lo tanto, y(n) = 0 para n 15.

En resumen, para la convolución tenemos

1.36 La correlación de dos sucesiones es una operación definida por la relación

Tenga en cuenta que usamos una estrella * para denotar correlación y un asterisco * para denotar convolución.

(a) Encuentre la correlación entre la secuencia x(n)=u(n)-u(n -6 ) y h(n)=u(n - 2) -u(n -5).

(b) Encuentre la correlación de x(n)=crnu(n)consigo mismo (es decir, h(n)=x(n)). Esto se conoce como la autocorrelación de x(n). Suponga que la1 < 1.

(a) Si comparamos la expresión de la correlación de x(n) y h(n) con la convolución

vemos que la única diferencia es que, en el caso de la convolución, h(k) se invierte en el tiempo antes de cambiar por n,

mientras que para la correlación h(k) se desplaza sin inversión de tiempo. Por lo tanto, con un grenfoque afico para calcular

la correlación, simplemente necesitamos graficar x(k) y h(k), desplazar h(k) por n (hacia la izquierda si n > 0 y hacia la derecha si

n < 0), multiplica las dos sucesiones x(k) y h(n + k), y suma los productos. En la siguiente figura se muestra un

gráfica de Fx(k) y h(k).

CAP. I] SEÑALES Y SISTEMAS

Denotando la correlación por r,h(n),es claro que para n =O la correlación es igual a 3. De hecho, esta será

el valor de rrh(n)para -I 5 n 5 2. Para n =3, s(k) y h(3 +k) solo se superponen en dos puntos, y rrh(3)=2.

De manera similar, debido a que x(k) y h(4 + k) solo se superponen en un punto, r,y,1(4)= I. Finalmente, rrh(n)=0 para n > 4.

Procediendo de manera similar para n < 0, encontramos que r,,,(-2) = 2, y r-,,,(-3)= 1. La correlación se muestra

en la figura de abajo.

~.vII(~)

(h) Sea r,(n) la autocorrelación de x(n), y observe que la autocorrelación es la convolución de x(n) con

x(-n):

Además observe que r,(n) es una función par de n:

Por lo tanto, solo es necesario encontrar los valores de r , (11) para n 10. Para n 2 0, tenemos

Usando la simetría de r,(n), tenemos, para n < 0,

Combinando estos dos resultados, finalmente tenemos

Ecuaciones de diferencias

1.37 Considere un sistema descrito por la ecuación en diferencias

Encuentre la respuesta de este sistema a la entrada

con condiciones iniciales y(-I) =0.75 y y(-2) =0.25.

El primer paso para resolver esta ecuación en diferencias es encontrar la solución particular. Con x(n) = (OS)"u(n),suponemos

una solución de la forma

y,(n) = Cl(0.5)" norte 2 0

Sustituyendo esta solución en la ecuación en diferencias, tenemos

SEÑALES Y SISTEMAS [CAP. 1

Dividiendo por (0.5)".

IC =2cI-4IC+o.5+1

lo que da

c,= ;

El siguiente paso es encontrar la solución homogénea. La ecuación característica es

z2-z+l=O

Por lo tanto, la forma de la solución homogénea es

yh(n)= ein"l> ~~~-1nnl3

y la solución total se convierte en

y(n) = (0.5)"+' + A, e~nnl> +2e-in+ nz0

Ahora se deben encontrar las constantes A1 y A2 para que la solución total satisfaga las condiciones iniciales dadas, y(-1) =

0,75 y y(-2) = 0,25. Debido a que la solución dada en la Ec. (1.25) solo es aplicable para n > 0, debemos derivar un

conjunto equivalente de condiciones iniciales para y(0) e y(l). Evaluando la ecuación en diferencias para n = 0 y n = I,

tener

y(0) = y(- 1) -y(-2) + OSx(0) + O.~X(- I) = 0,75 -0,25 + 0,5 = 1

y

y(l) = y(0) - y(-1) + 0,5~(1)+ OSx(0) = 1 -0,75 + 0,25 +0,5 = 1

Ahora, sustituyendo estas condiciones iniciales derivadas en la Ec. (1.25), tenemos

y(O) = 0.5 + Al + A2 = Yo

y(I) = 0,25 + A,ei"I3 + ~ ~ = 1 e - ~ ~ ~ ~

Escribiendo este par de ecuaciones en las dos incógnitas A I y A2 en forma matricial,

y resolviendo encontramos .~5 $~jn/3 - 2

[::I =IT [-teinp+;]

Sustituyendo en la Ec. (1.25) y simplificando, encontramos, después de un poco de álgebra.

Una observación importante que hacer sobre esta solución es que. porque la ecuación en diferencia tiene coeficientes reales,

las raíces del polinomio característico están en pares complejos conjugados. Esto asegura que la respuesta de la muestra unitaria

es real. Con una entrada de valor real x(n), la respuesta debe ser real y, por lo tanto, se deduce que A2 será el complejo

conjugado de A 1 :

1.38 El LCCDE describe un sistema recursivo de segundo orden

(a) Encuentre la respuesta muestral unitaria h(n) de este sistema.

(h) Encuentre la respuesta del sistema a la entrada x(n) = u(n) - u(n - 10) con condiciones iniciales cero.

CAP. I] SEÑALES Y SISTEMAS

(c) Encuentre la respuesta del sistema a la entrada x(n) = (;)"u(n) con condiciones iniciales cero.

(a) Para encontrar la respuesta de la muestra unitaria, debemos resolver la ecuación en diferencias con x(n)=S(n) y descanso inicial

condiciones. La ecuación característica es

Por lo tanto, la solución homogénea es

Como la solución particular es cero cuando la entrada del sistema es una muestra unitaria, la Ec. (1.26) representa el total

solución.

Para encontrar las constantes Al y A2, debemos derivar las condiciones iniciales en n = 0 y n = I. Con reposo inicial

condiciones, y(- I) = y(-2) = 0, se sigue que

Ahora podemos escribir dos ecuaciones en las dos incógnitas A1 y A2 evaluando la ecuación. (1.26) en n = 0 y n = I

como sigue:

Resolviendo para Al y A2, encontramos

A,=-2 A2=3

De este modo,

y(n) = -2(i)" + 3($)" n 2 o

y la respuesta de la muestra unitaria es

h(n)= [-2(;)" + 3(a)"]u(n)

(b) Para encontrar la respuesta del sistema a x(n) = u(n)-u(n - lo), podemos proceder de una de dos maneras. Primero nosotros

puede realizar la convolución de h(n) con x(n):

Alternativamente, observando que la entrada es una suma de dos pasos, podemos encontrar la respuesta al escalón del sistema, s(n), y

luego usando la linealidad. escribir la respuesta como

Usando este enfoque, vemos en la parte (a) que la respuesta al escalón para n 0 es

Evaluar las sumas usando la serie geométrica. encontramos

Por lo tanto, la solución deseada es

11-10

y(n) = s(n) -s(n - 10) = [2(f)" -(:)"]u(n) -[2(f) -(i)n-lo]u(n - 10)

SEÑALES Y SISTEMAS [CAP. I

(c) Con x(n) = (f)"u(n), observe que .r(n) tiene la misma forma que uno de los términos en la solución homogénea.

Por lo tanto, la solución particular no será de la forma y,(n) = C(:)" como se indica en la tabla 1-2. Si fuéramos

sustituir esta solución particular en la diferencia equación, encontraríamos que ningún valor de C funcionaría.

Como ocurre cuando una raíz de la ecuación característica es de segundo orden, la solución particular tiene la forma

yp(n) = cn(!)''

Sustituyendo esto en la ecuación en diferencias, tenemos

Dividiendo entre (f )I1, tenemos

Resolviendo para C, encontramos que C = -2. Por lo tanto, la solución total es

Ahora debemos resolver para las constantes A1 y A> Como hicimos en la parte (a), con condiciones iniciales cero encontramos que

y(0) = I y y(l) = $. Por lo tanto, al evaluar la ecuación. (1.27) en 11 = 0 y n = 1, obtenemos los siguientes dos

ecuaciones en las dos incógnitas Al y A2:

Resolviendo para A1 y Az, encontramos que A1 = 4 y A2 = 3. Por lo tanto, la solución total se convierte en

1.39 Una hipoteca de $100 000 debe pagarse en pagos mensuales iguales de d dólares. Interés, compuesto

mensual, se cobra a una tasa del 10 por ciento anual sobre el saldo impago [por ejemplo, después del primer mes

la deuda total es igual a ($100 000 + ~$100 000)]. Determine el monto del pago, d, de modo que el

hipoteca se paga en 30 años, y encuentre la cantidad total de pagos que se hacen durante los 30 años

período.

El saldo total impago al final del enésimo mes. en ausencia de préstamos o pagos adicionales, es igual

al saldo insoluto del mes anterior más los intereses cobrados sobre el saldo insoluto del mes anterior.

Por lo tanto, con y(n) el saldo al final del mes n tenemos

donde B = es el interés cobrado sobre el saldo insoluto. Además, el saldo debe ser ajustado por el neto

cantidad de dinero que sale del banco en su bolsillo, que es simplemente la cantidad prestada en el mes n menos

la cantidad pagada al banco en el mes n. De este modo

donde xb(n) es la cantidad prestada en el mes n y xp(n) es la cantidad pagada en el mes n. Combinatorio

términos, tenemos

y(n) - vy(r - 1) =xh(n) -x,,(n) =x(n)

donde v = I + B = 1 + 9, y x(n) es la cantidad neta de dinero en el mes n que sale del banco. Porque

se pide prestado un principal de p dólares durante el mes cero, y los pagos de d dólares comienzan con el mes I, el impulsor

función, x(n), es

x(n) = .wh(n)-.u,,(n) = p8(n) - du(n - 1)

y la ecuación de diferencias para y(n) se convierte en

CAP. I] SEÑALES Y SISTEMAS 47

Debido a que asumimos condiciones iniciales cero, y(- 1) = 0, y debido a que la entrada consiste en una combinación lineal

de una muestra unitaria escalada y un paso retrasado escalado, la solución a la ecuación en diferencias es simplemente

donde h(n) y s(n) son la muestra unitaria y la respuesta al escalón unitario, respectivamente. Para encontrar la respuesta de la muestra unitaria,

escribir la ecuación en diferencia en la forma

La ecuación característica de esta ecuación en diferencias es

y la solución homogénea es

y(n)=Avn n>O

Como la entrada x(n) = S(n) es igual a cero para n > 0, la solución particular es cero (todo lo que hace la muestra unitaria

se establece la condición inicial en n = 0). Evaluando la ecuación en diferencias en n = 0, tenemos

Por lo tanto, se sigue que A = 1 en la solución homogénea y que la respuesta de la muestra unitaria es

La respuesta al escalón ahora se puede encontrar convolucionando h(n) con u(n):

Por lo tanto, la solución total es

Ahora queremos encontrar el valor de d para que después de 360 pagos mensuales iguales, la hipoteca esté pagada. En otra

palabras. queremos encontrar d tal que

Resolviendo, ford, tenemos

Con v = % y p = 100.000, tenemos

d = 877,57

El pago total al banco después de 30 años es

C = (877,57)(360) = 315.925,20

1.40 Cada segundo, cada partícula a dentro de un reactor se divide en ocho partículas P y cada partícula L3 se divide en

una partícula LY y dos partículas P. Esquemáticamente,

a+8P P-a+2/3

SEÑALES Y SISTEMAS [CAP. 1

Dado que hay una sola partícula a en el reactor en el tiempo n = 0, encuentre una expresión para el número total

de partículas dentro del reactor en el tiempo n.

Sean a(n) y B(n) el número de partículas a y partículas B dentro del reactor en el tiempo n. El comportamiento dentro de la

El reactor puede describirse mediante el siguiente par de ecuaciones en diferencias acopladas:

Antes de que podamos resolver estas ecuaciones en diferencias, debemos desacoplarlas. Por lo tanto, deduzcamos una sola diferencia

ecuación para B(n). De la primera ecuación vemos que a(n) = #?(n -I). Sustituyendo esta relación en la segunda

ecuación en diferencias, tenemos

B(n+ 1)=8B(n-1)+2B(n)

o equivalente,

B(n)= 2B(n - 0 + 8B(n -2)

La ecuación característica de esta ecuación en diferencias es

lo que da la siguiente solución homogénea

De manera similar, debido a que a(n) = B(n -I), la solución para a(n) es

Con las condiciones iniciales a(0) = I y B(0) = 0, podemos resolver para A1 y A2 de la siguiente manera:

y las soluciones para a(n) y B(n) son

a(n) = i(4)" + !(-2)" norte 2 0

B(n) = :(4)" - ?(-2)" 3 norte 2 0

Porque estamos interesados en el número total de partículas dentro del reactor en el tiempo n, con

Problemas complementarios

Señales de tiempo discreto

1.41 Encuentra el periodo N de la sucesión

CAP. 11 SEÑALES Y SISTEMAS

1.42 La entrada a un sistema lineal invariante por corrimiento es periódica con período N.

(a) Demuestre que la salida del sistema también es periódica con período N.

(b) Si el sistema es lineal but variable por turnos, ¿se garantiza que la salida sea periódica?

(c) Si el sistema no es lineal pero no varía con el desplazamiento, ¿se garantiza que la salida sea periódica?

1.43 Si x(n) = 0 para n < 0, y la parte impar es x(n) = n(0.5)1n1, encuentre x(n) dado que x(0) = 1.

1.44 Encuentra la parte simétrica conjugada de la secuencia

1.45 Si x(n) es impar, ¿cuál es y(n) = x2(n)?

1.46 Si x(n) = 0 para n < 0, Pe es la potencia de la parte par de x(n), y Po es la potencia de la parte impar, ¿cuál de las

siguientes afirmaciones son verdaderas?

(a) PC? Correos

(b) Po 2 Pe

c) Pe = Po

(d) Ninguna de las anteriores es cierta.

1.47 Expresar la secuencia

(-1 x(n) = (0

-2 5 11 5 2

demás

como una suma de pasos unitarios escalados y desplazados.

1.48 Sintetizar el pulso triangular

como una suma de pulsos escalados y desplazados,

Sistemas de tiempo discreto

1.49 A continuación se enumeran varios sistemas que relacionan la entrada x(n) con la salida y(n). Para cada uno, determine si el

el sistema es lineal o no lineal, invariante o variable, estable o inestable, causal o no causal e invertible

o no inversora.

(e) y(n) = mediana(x(n -l), x(n), x(n + I))

SEÑALES Y SISTEMAS [CAP. 1

A continuación se presentan las respuestas de muestra unitaria de varios sistemas lineales invariantes por desplazamiento. Para cada sistema, determine la

condiciones sobre el parámetro a para que el sistema sea estable.

(a) h(n) = anu(-n)

(h) h(n) = a"[u(n)-u(n - 100))

(c) h(n) = aInl

¿Es cierto que todos los sistemas sin memoria son invariantes al cambio?

Considere el sistema lineal invariante de desplazamiento descrito por la ecuación de diferencia de coeficiente constante lineal de primer orden

y(n) = uy(n -I) + x(n)

Determine las condiciones (si las hay) para las cuales este sistema es estable.

Suponga que dos sistemas, SI y SZ, están conectados en paralelo.

(a) Si tanto S, como Sz son lineales, invariantes al desplazamiento, estables. y causal, la conexión paralela será siempre lineal,

invariante al cambio, estable. y causales?

(h) Si tanto S como Sz son no lineales. ¿La conexión en paralelo será necesariamente no lineal?

(c) Si tanto SI como S2 varían según el desplazamiento, ¿la conexión en paralelo será necesariamente variable según el desplazamiento?

Circunvolución

Encuentre la convolución de las dos secuencias.

s(n) = 6(n -2 ) -26(n -4) + 36(n -6)

h(n) = 2S(n + 3) + S(n)+ 26(n - 2 )+ 6(n

La respuesta de la muestra unitaria de un sistema lineal invariante por desplazamiento es

h(n)= 36(n - 3) + 0.5S(n -4) + 0.26(n -5) + 0.76(n.

Encuentre la respuesta de este sistema a la entrada x(n) = u(n -I).

Un sistema lineal invariante por desplazamiento tiene una respuesta de muestra unitaria

h(n)= u(-n)

Encuentre la salida si la entrada es

A-(n)= (i)"rc(n)

La respuesta al escalón de un sistema se define como la respuesta del sistema a un escalón unitario u(n).

(a) Sea s(n) la respuesta escalonada de un sistema lineal invariante por desplazamiento. Exprese s(n)en términos de la respuesta de la muestra unitaria

h(n), y encuentre s(n) cuando h(n) = u(n)-u(n -6).

(b) Deduzca una expresión para h(n) en términos de s(n) y encuentre la respuesta de la muestra unitaria Para un sistema cuyo paso

la respuesta es

A continuación se muestra la respuesta de la muestra unitaria de un sistema lineal invariante por desplazamiento.

CAP. 11 SEÑALES Y SISTEMAS

(a) Encuentre la respuesta del sistema a la entrada u(n -4).

(6) Repita para x(n) = (-l)"u(n).

Si x(n) = (i)"u(n -2) y h(n) = 2"u(-n -5), encuentre la convolución y(n) = x(n) * h(n).

Dadas tres secuencias, h(n), g(n) y r(n), exprese g(n) en términos de r(n) si

Sean h(n) = anu(n) y x(n) = bnu(n). Encuentre la convolución y(n) = x(n)* h(n) suponiendo que a # 6.

Si x(n) = anu(n), encuentre la convolución y(n) = x(n) * x(n).

La entrada a un sistema lineal invariante por desplazamiento es el escalón unitario, x(n) = u(n), y la respuesta es y(n) = S(n). Encuentra el

respuesta muestral unitaria de este sistema.

Si h(n) = A6(n)+(f )"u(n) es la respuesta de muestra unitaria de un sistema lineal invariante por desplazamiento, y s(n) es la respuesta escalonada

(la respuesta del sistema a un escalón unitario), encuentre el valor de la constante A tal que lím,,, s(n) = 0.

La respuesta de la muestra unitaria de un sistema lineal invariante por desplazamiento es

Encuentra la respuesta del sistema a la exponencial compleja x(n) = exp(jnrr/4).

Evalúa la convolución de la sucesión x(n) = n(i)"cos(rrn) con el escalón unitario, h(n) = u(n).

Dejar

n(0.5)" 0 5 n 5 5

suboficial

y h(n) = ej%"u(-n). Si y(n) = x(n) * h(n), ¿cuál es el valor numérico de y(-2)?

Dado

y h(n) = S(n - 2) + S(n - 3) + 6(n -4), ¿a qué valor de n alcanzará la convolución y(n) = x(n) * h(n) es

valor máximo, y cuál es este valor máximo?

Un sistema lineal tiene una respuesta hk(n)= S(2n -k) a la muestra unitaria 6(n - k). Encuentre la respuesta del sistema a

la entrada x(n) = u(n).

Considere la interconexión de tres sistemas lineales invariantes por desplazamiento que se muestran en la siguiente figura.

- hAn)

1I

+

x(n) : h~(n) - (+> = ~(n)

+

11

-- h3(n)

SEÑALES Y SISTEMAS [CAP. 1

Si hl(n) = u(n - 2), hn(n) = nu@) y h3(n) =6(n - 2). Encuentre la respuesta muestral unitaria del sistema total.

Ecuaciones de diferencias

1.71 Considere el sistema lineal invariante por desplazamiento descrito por LCCDE

y(n) = -iy(n -I) +2x(n)

Encuentre la respuesta de este sistema a la entrada

x(n) =

2

0

n=0,2,4,6 ,...

de lo contrario

Pista: Escribe x(n) como (1 +(-1)") u(n) y usa la linealidad.

1.72 Considere un sistema con entrada x(n) y salida y(n) que satisface la ecuación en diferencias

y(n) =ny(n -I) +x(n)

Si x(n) =6(n), determine y(n) para todo n.

1.73 El LCCDE describe un sistema lineal invariante por desplazamiento

y(n)-5y(n-I)+6y(n-2) =x(n-1)

Encuentre la respuesta escalonada del sistema (es decir, la respuesta a la entrada x(n) = u(n)).

1.74 Un sistema se caracteriza por la ecuación en diferencias

Si la entrada es x(n) =2u(n) - 3nu(n), encuentre la respuesta del sistema suponiendo condiciones iniciales de y(-1) = 2 y

y(-2) = 1.

1.75 Considere el sistema descrito por la ecuación en diferencia

y(n) - y(n - 1) +0.25y(n -2) =x(n) - 0.25x(n - 1)

(a) Encuentre la respuesta muestral unitaria del sistema.

(b) Encuentre la respuesta del sistema a x(n) = (0.25)"u(n).

1.76 Para una cuenta de ahorros que paga intereses a razón del uno por ciento mensual, si los depósitos se hacen el primero de cada

mes a razón de $50 por mes, ¿cuánto dinero habrá en la cuenta al final de 1 año?

1.77 Una cuenta de ahorros paga intereses a una tasa de 1 por ciento mensual. Con un depósito inicial de $50, ¿cuánto costará

habrá en la cuenta después de 10 años?

Respuestas a problemas complementarios

1.42 (a) Si x(n) =x(n + N), por cambio de invariancia, y(n) =y(n + N). Por lo tanto, y(n) es periódico con período N.

(b) No. (c) Sí.

CAP. 11 SEÑALES Y SISTEMAS

1,45 pares.

1.46 (a) es verdadera.

1.49 (a) Lineal, cambiante, estable, no causal, no invertible. (6) Lineal, cambiante, inestable, no causal,

invertible (c) Lineal, invariante al cambio, estable. no causal, invertible. (d) No lineal, invariante al cambio, estable, causal,

invertible (0) No lineal, invariante al cambio, estable, no causal, no invertible.

1.50 (a) la1 1. (6) Cualquier finito a. (c) la[ < 1.

1.51 No. Considere el sistema y(n) = x(n)cos(nr/2).

1.53 a) Sí. (6) No. (c) No.

1.54 Los valores de secuencia. comenzando en el índice n = -I, son y(n) = {2,0, -4, 1,6,0, I, -1, -2,6,3).

norte

1.57 (a) s(n) = h(k). Con h(n) = u(n) - u(n -6) la respuesta al escalón es

k=-cc

(6) h(n) = s(n) -s(n - 1). Si s(n) = (-0.5)nu(n), entonces h(n) = S(n) + 3(-0.5)"u(n - 1).

1.58 (a) y(n) = S(n -2) + 2S(n - 3) -2S(n -5) -S(n -6).

(b) y(n) = S(n + 2) - 26(n) + S(n -2).

bn+l - an+l

1.61 y(n) = -- u(n). Ja

1.63 h(n) = S(n) -S(n -I).

54 SEÑALES Y SISTEMAS [CAP. 1

y(n) = [(4n+3)(-i)" -3]u(n).

y(-2) = 17 -jns* 4 32

max(y(n)]= y , que ocurre en el índice n = 8.

y(n) = 4n).

Y@)= u(n -4 )+ f (n -2)(n - 1) u(n -2).

y(n) = [4(-1)" + - !(-f)"]u(n).

y(n) = n! Naciones Unidas).

~(n) = [i + (;)(3)" - 2(2")]u(n).

~(n) = [lj?.[4"- 11 -4n + 12(2)"]u(n).

(0) h(n)= [en + ~](i)~u(n). (b) y(n) = (n+ I )(f)nu(n).

$690,46.

$165,02.

Capítulo 2. Análisis de Fourier 

2.1 Introducción 

 La representación de Fourier de señales juega un papel extremadamente importante tanto en tiempo continuo como en tiempo discreto. procesamiento de la señal. Proporciona un método para mapear señales en otro "dominio" en el que manipularlas. Lo que hace que la representación de Fourier sea particularmente útil es la propiedad de que la operación de convolución se mapea a la multiplicación. Además, la transformada de Fourier proporciona una forma diferente de interpretar señales y sistemas.

En este capítulo desarrollaremos la transformada de Fourier en tiempo discreto (es decir, una transformada de Fourier para señales). Mostraremos cómo las exponenciales complejas son funciones propias de sistemas lineales invariantes por desplazamiento (LSI) y cómo esta propiedad conduce a la noción de una representación de respuesta de frecuencia de los sistemas LSI. Finalmente nosotros explorará cómo se puede usar la transformada de Fourier en tiempo discreto para resolver la diferencia de coeficiente constante lineal ecuaciones y realizar convoluciones.

2.2 Respuesta de frecuencia 

  Las funciones propias de los sistemas lineales invariantes por desplazamiento son secuencias que, cuando ingresan al sistema, pasan con solo un cambio en la amplitud (compleja). Es decir, si la entrada es x(n), la salida es y(n) = kx(n), donde A, el valor propio, generalmente depende de la entrada x(n).

Señales de la forma

~(n)= ejnw -00€n<ca

donde w es una constante, son funciones propias de los sistemas LSI. Esto se puede mostrar a partir de la suma de convolución

Por lo tanto, el valor propio, que denotamos por H (elw), es

 

Nótese que H(eJw) es, en general, de valor complejo y depende de la frecuencia w de la exponencial compleja.

Por lo tanto, puede escribirse en términos de sus partes real e imaginaria.

 o en términos de su magnitud y fase, 

Donde 

 y

Las representaciones gráficas de la respuesta de frecuencia son de gran valor en el análisis de los sistemas LSI, y comúnmente se utilizan gráficos de la magnitud y la fase. Sin embargo, otra representación gráfica útil es un diagrama de 20 log1H(eJ")I frente a o. Las unidades en la escala logarítmica de magnitud son decibelios (dB abreviado). Así, 0 dB corresponde a un valor de 1H(ejW)l= 1,20dB es equivalente a 1H(ejw) l = 10, -20dB es equivalente a IH(ejU)l = 0,1, etcétera. También es útil notar que 6 dB corresponde aproximadamente a I H (eJ")( = 2, y -6 dB es aproximadamente I H(eJW)l= 0.5. Una de las ventajas de una gráfica de magnitud logarítmica es que, debido a que el logaritmo expande el escala para valores pequeños de (H(ej")), es útil para mostrar los detalles finos de la respuesta de frecuencia cercana a cero.

Una representación gráfica que se usa a menudo en lugar de la fase es el retardo de grupo, que se define como sigue: 

Al evaluar el retardo de grupo, la fase se toma como una función continua y diferenciable de w sumandomúltiplos enteros de n al valor principal de la fase (esto se conoce como desenvolver la fase). La función ~(ej") es muy útil e importante en la caracterización de sistemas LSI y se llamala respuesta de frecuencia La respuesta de frecuencia define cómo se cambia un exponencial complejo en (complejo) amplitud cuando es filtrado por el sistema. La respuesta de frecuencia es particularmente útil si somos capaces de descomponer una señal de entrada en una suma de exponenciales complejos. Por ejemplo, la respuesta de un sistema LSI a una entrada de la forma 

 sera 

donde H(ejw) es la respuesta en frecuencia del sistema evaluado a la frecuencia on.

EJEMPLO 2.2.1 Sea x(n) = cos(n*) la entrada de un sistema lineal invariante por desplazamiento con una muestra unitaria de valor real respuesta h(n). Si x(n) se descompone en una suma de dos exponenciales complejas, 

 la respuesta del sistema puede escribirse como 

Debido a que h(n) tiene un valor real, H(eJW) es simétrica conjugada: 

Por lo tanto, 

y se sigue que 

Periodicidad

La respuesta de frecuencia es una función de valor complejo de w y es periódica con un período 23r. esto es en agudo contrasta con la respuesta de frecuencia de un sistema de tiempo continuo lineal e invariante en el tiempo, que tiene una frecuencia

respuesta que no es periódica, en general. La razón de esta periodicidad surge del hecho de que un tiempo discreto exponencial compleja de frecuencia oo es lo mismo que exponencial compleja de frecuencia wo + 23r; eso es, 

 Por lo tanto, si la entrada a un sistema lineal invariante por desplazamiento es x(n) = ejnWO, la respuesta debe ser la misma que la

respuesta a la señal s(n) = eJn(w+2n). Esto, a su vez, requiere que 

Simetría

Si h(n) tiene un valor real, la respuesta de frecuencia es una función de frecuencia simétrica conjugada:

H (e-jw) = H *(ejw)

La simetría conjugada de H(ejW) implica que la parte real es una función par de w,

FC(ejW)= FC(eCi")

y que la parte imaginaria es impar,

Hl(ejW)= -~[(e-j")

La simetría conjugada también implica que la magnitud es par,

IH (ejW)l= IH (e-j") 1

y que el retardo de fase y de grupo son impares

Considere el sistema LSI con respuesta de muestra unitaria

donde a es un número real con la1 < I. La respuesta de frecuencia es 

La magnitud al cuadrado de la respuesta de frecuencia es 

 la fase

 Finalmente, el retardo de grupo se encuentra diferenciando la fase. El resultado es 

Invertir la respuesta de frecuencia

Dada la respuesta de frecuencia de un sistema lineal invariante por desplazamiento,

la respuesta de la muestra unitaria se puede recuperar por integración: 

La integral puede tomarse sobre cualquier período de longitud 2n.

EJEMPLO 2.2.3 Para un sistema con una respuesta en frecuencia dada por 

(este sistema se denomina filtro de paso bajo ideal), la respuesta de la muestra unitaria es

,

Tenga en cuenta que este sistema no es causal (también es inestable) y, por lo tanto, irrealizable.

2.3 Filtros 

 El término filtro digital, o simplemente filtro, se usa a menudo para referirse a un sistema de tiempo discreto. Se define un filtro digital por J. E Kaiser1 como un "...proceso computacional o algoritmo por el cual una señal muestreada o secuencia de números (que actúa como entrada) se transforma en una segunda secuencia de números denominada señal de salida. El proceso computacional puede ser filtrado de paso bajo (suavizado), filtrado de paso de banda, interpolación, generación de  derivados, etc.”

Los filtros se pueden caracterizar en términos de sus propiedades del sistema, tales como linealidad, cambio de invariancia, causalidad, estabilidad, etc., y pueden clasificarse en función de la forma de su respuesta en frecuencia. Algunos de estos las clasificaciones se describen a continuación.

Fase lineal

Se dice que un sistema lineal invariante por desplazamiento tiene fase lineal si su respuesta de frecuencia es de la forma ~(ei")= A(ejw)mandíbula electrónica donde ar es un número real y ~(ej") es una función de valor real de w. Nótese que la fase de H(ei") es 

De manera similar, se dice que un filtro tiene fase lineal generalizada si la respuesta de frecuencia tiene la forma 

Por lo tanto, los filtros con fase lineal o fase lineal generalizada tienen un retardo de grupo constante

Todo pasa

Se dice que un sistema es un filtro de paso total si la magnitud de la respuesta de frecuencia es constante:

1H(eJ")l = c

Un ejemplo de un filtro de paso total es el sistema que tiene una respuesta de frecuencia

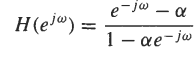
 donde ct es cualquier número real con la1 < I. La respuesta de muestra unitaria de este filtro de paso total es 

Filtros selectivos de frecuencia

Muchos de los filtros que son importantes en las aplicaciones tienen magnitudes de respuesta de frecuencia constantes por tramos. Estos incluyen los filtros de paso bajo, paso alto, paso de banda y supresión de banda que se ilustran en la figura 2-1. los intervalos sobre las cuales la magnitud de la respuesta de frecuencia es igual a 1 se denominan bandas de paso, y los intervalos sobre los cuales es igual a 0 se llaman bandas de parada. Las frecuencias que marcan los bordes de las bandas de paso y de parada son las frecuencias de corte.

 para bajas ideal 

 pasa altas ideal 

 pasa bandas ideal 

 rechaza bandas ideal

2.4 Interconexión de Sistemas 

 Los filtros a menudo se interconectan para crear sistemas que tienen propiedades deseables. Dos tipos comunes de conexiones son serie (cascada) y paralelo. En la siguiente figura se muestra una cascada de dos sistemas lineales invariantes por desplazamiento. 

Una cascada es equivalente a un solo sistema lineal invariante de desplazamiento con una respuesta de muestra unitaria h(n)= h1(n)*h2(n)

respuesta en frecuencia 

Tenga en cuenta que la magnitud logarítmica de la cascada es la suma de las magnitudes logarítmicas de los sistemas individuales, 

 y el retardo de fase y de grupo son aditivos,

En la siguiente figura se muestra una conexión en paralelo de dos sistemas lineales invariantes al desplazamiento.

Una red paralela es equivalente a un solo sistema lineal invariante de desplazamiento con una respuesta de muestra unitaria

Por lo tanto, la respuesta de frecuencia de la red paralela es

EJEMPLO 2.4.1 La cascada de un filtro de paso bajo con un filtro de paso alto se puede utilizar para implementar un filtro de paso de banda. Para  ejemplo, el filtro de paso de banda ideal que se muestra en la Fig. 2-I(c) puede realizarse conectando en cascada un filtro de paso bajo con una frecuencia de corte y con un filtro de paso alto que tiene una frecuencia de corte w,. De manera similar, el filtro de supresión de banda que se muestra en la Fig. 2-l(d) puede realizarse con un conexión en paralelo de un filtro de paso bajo con frecuencia de corte w 1 y un filtro de paso alto con frecuencia de corte y, con y > wl. Otra interconexión de sistemas que se encuentra comúnmente en aplicaciones de control es la red de retroalimentación.se muestra en la siguiente figura 

podemos usar las técnicas de análisis de Fourier descritas en la siguiente sección para mostrar que la respuesta de frecuencia de este sistema, si existe, es

2.5 La transformada de Fourier en tiempo discreto 

 La respuesta de frecuencia de un sistema lineal invariante al desplazamiento se encuentra multiplicando h(n) por una exponencial compleja, e-Jn", y sumando sobre n. La transformada de Fourier en tiempo discreto (DTFT) de una secuencia, x(n), se define en el mismo camino, 

Por lo tanto, la respuesta de frecuencia de un sistema lineal invariante por desplazamiento, ~(ej"), es la DTFT de la respuesta de la muestra unitaria, h(n). Para que exista la DTFT de una secuencia, la suma en Eq. (2.3) debe converger. Esto a su vez, requiere que x(n) sea absolutamente sumable:

EJEMPLO 2.5.1 La DTFT de la secuencia

Usando la serie geométrica, esta suma es 

la DTFT es 

Cambiando los límites de la suma, tenemos 

Si lal > 1, esta suma es 

Por lo tanto, x,(n) = anu(n) y x2(n) = -anu(-n -I) ambos tienen la misma DTFT.

~es posible que g(n) haga que el sistema sea inestable, en cuyo caso la DTFT de h(n) no existirá. Los sistemas de retroalimentación son típicamente analizado usando transformadas z

Dado X(eJw), la secuencia x(n) puede recuperarse usando la DTFT inversa, 

La DTFT inversa puede verse como una descomposición de x(n) en una combinación lineal de todas las exponenciales complejas que tienen frecuencias en el rango -17 iw 5 IT. La Tabla 2-1 contiene una lista de algunos pares DTFT útiles. 

Tabla 2-1 Algunos pares DTFT comunes

Transformada de Fourier de tiempo discreto de secuencia

EJEMPLO 2.5.2 Suponga que X(eJ") consiste en un impulso de frecuencia w = wo: 

Usando el DTFT inverso, tenemos 

Tenga en cuenta que aunque x(n) no es absolutamente sumable, al permitir que la DTFT contenga impulsos, podemos considerar que la DTFT de sucesiones que contienen exponenciales complejas. Como otro ejemplo, si 

Calculando la DTFT inversa, encontramos

2.6 Propiedades DTFT 

 Hay una serie de propiedades de la DTFT que se pueden utilizar para simplificar la evaluación de la DTFT y su inverso. Algunas de estas propiedades se describen a continuación. En la Tabla 2-2 aparece un resumen de las propiedades de DTFT.

Periodicidad

La transformada de Fourier de tiempo discreto es periódica en w con un período de 2n: 

Esta propiedad se deriva directamente de la definición de la DTFT y la periodicidad de las exponenciales complejas: 

Tabla 2-2 Propiedades de la DTFT

Secuencia de propiedades de la Transformada de Fourier de tiempo discreto

linealidad

Cambio

Inversión del tiempo

Modulación

Circunvolución

Conjugación

Derivado

Multiplicación

Nota: Dadas las DTFT X(eJW) e Y(eJW) de x(n) e y(n), esta tabla enumera las DTFT de secuencias que se forman a partir de x(n) e y(n).

Simetría

La DTFT a menudo tiene algunas simetrías que pueden aprovecharse para simplificar la evaluación de la DTFT o la DTFT inversa. Estas propiedades se enumeran en la siguiente tabla.

Real e incluso Real e incluso

Real y extraño Imaginario y extraño

Imaginario e incluso Imaginario e incluso

Imaginario y extraño Real y extraño

Tenga en cuenta que estas propiedades se pueden combinar. Por ejemplo, si x(n) es simétrica conjugada, su parte real es

par y su parte imaginaria es impar. Por lo tanto, se sigue que X(eJW) es de valor real. De manera similar, tenga en cuenta que si x(n)

es real, la parte real de x(ejw) es par y la parte imaginaria es impar. Por tanto, X(ejw) es simétrica conjugada.

linealidad

La transformada de Fourier de tiempo discreto es un operador lineal. Es decir, si X 1 (ejw) es la DTFT de xl(n), y  X2(eJw) es la DTFT de x2(n) 

Propiedad cambiante

Desplazar una secuencia en el tiempo da como resultado la multiplicación de la DTFT por una exponencial compleja (fase lineal término): 

Inversión del tiempo

La inversión de tiempo de una secuencia da como resultado una inversión de frecuencia de la DTFT:

Modulación

Multiplicar una secuencia por un exponencial complejo da como resultado un cambio en la frecuencia de la DTFT: 

Por lo tanto, modular una secuencia por un coseno de frecuencia % desplaza el espectro hacia arriba y hacia abajo en frecuencia por oo: 

Teorema de convolución

Quizás el resultado más importante de la teoría de sistemas lineales es que la convolución en el dominio del tiempo es equivalente a la multiplicación en el dominio de la frecuencia. Específicamente, este teorema dice que la DTFT de una secuencia que es formada por la convolución de dos secuencias, x(n) y h(n), es el producto de las DTFT de x(n) y h(n):

Teorema de la multiplicación (convolución periódica)

Al igual que con las propiedades de cambio de tiempo y modulación, hay un dual en el teorema de convolución que establece que la multiplicación en el dominio del tiempo corresponde a la convolución (periódica) en el dominio de la frecuencia:

Teorema de Parseval

Un corolario del teorema de la multiplicación es el teorema de Parseval, que es

El teorema de Parseval se conoce como el teorema de conservación de la energía, porque establece que el operador DTFT conserva la energía cuando se pasa del dominio del tiempo al dominio de la frecuencia.

2.7 Aplicaciones 

 En esta sección, presentamos algunas aplicaciones de la DTFT en el análisis de señales en tiempo discreto. Estos incluyen encontrar la respuesta de frecuencia de un sistema LSI que se describe mediante una ecuación en diferencia, realizando convoluciones, resolver ecuaciones en diferencias que tienen condiciones iniciales cero y diseñar sistemas inversos.

2.7.1 Sistemas LSI y LCCDE 

 Una subclase importante de sistemas LSI contiene aquellos cuya entrada, x(n), y salida, y(n), están relacionadas por una relación lineal. ecuación de diferencia de coeficiente constante (LCCDE) 

Las propiedades de linealidad y cambio de la DTFT pueden usarse para expresar esta ecuación de diferencia en la frecuencia dominio de la siguiente manera: 

o

Por lo tanto, la respuesta de frecuencia de este sistema es 

EJEMPLO 2.7.1 Considere el sistema lineal invariante por desplazamiento caracterizado por el coeficiente constante lineal de segundo ordenecuación diferencial 

La respuesta de frecuencia se puede encontrar mediante inspección sin resolver la ecuación de diferencia para h(n) de la siguiente manera:

Tenga en cuenta que este problema también se puede trabajar en la dirección inversa. Por ejemplo, dada una función de respuesta de frecuencia como

se puede encontrar fácilmente una ecuación en diferencias que implemente este sistema. Primero, dividiendo numerador y denominador por 2 y reescribiendo la respuesta de frecuencia de la siguiente manera,

we see that a difference equation for this system is 

2.7.2 Realización de circunvoluciones 

 Debido a que la DTFT mapea la convolución en el dominio del tiempo en la multiplicación en el dominio de la frecuencia, la DTFT proporciona una alternativa para realizar convoluciones en el dominio del tiempo. El siguiente ejemplo ilustra la procedimiento.

EJEMPLO 2.7.2 Si la respuesta de muestra unitaria de un sistema LSI es

la DTFT de y (n) es

Por lo tanto, todo lo que se requiere es encontrar la DTFT inversa de Y (el"). Esto se puede hacer fácilmente expandiendo Y (ej") de la siguiente manera: 

donde A y B son constantes que se van a determinar. Expresando el lado derecho de esta expansión sobre un común denominador, 

e igualando los coeficientes, las constantes A y B se pueden encontrar resolviendo el par de ecuaciones 

El resultado es 

Por lo tanto,

Y se deduce que la DTFT inversa es 

2.7.3 Resolver ecuaciones en diferencias 

 En el cap. 1 vimos métodos para resolver ecuaciones en diferencias en el "dominio del tiempo". La DTFT puede ser se utiliza para resolver ecuaciones en diferencias en el "dominio de la frecuencia" siempre que las condiciones iniciales sean cero. El El procedimiento consiste simplemente en transformar la ecuación en diferencias en el dominio de la frecuencia tomando la DTFT de cada término en la ecuación, resolviendo el término deseado y encontrando la DTFT inversa.

EJEMPLO 2.7.3 Resolvamos el siguiente LCCDE para y(n) suponiendo condiciones iniciales cero,

para x(n) = &). Comenzamos tomando la DTFT de cada término en la ecuación en diferencias:

Como la DTFT de x(n) es X(ejw) = 1,

Usando el par DTFT

la DTFT inversa de Y (ej ") se puede encontrar fácilmente usando las propiedades de linealidad y cambio,

2.7.4 Sistemas Inversos

 El inverso de un sistema con respuesta de muestra unitaria h(n) es un sistema que tiene una respuesta de muestra unitaria g(n) tal que En términos de la respuesta de frecuencia, es fácil ver que, si existe el inverso de H(eJm), es igual a 

Sin embargo, se debe tener cuidado porque no todos los sistemas son invertibles o, si existe la inversa, puede ser no causal Por ejemplo, el filtro de paso bajo ideal del Ejemplo 2.2.3 no tiene inversa, y la inversa de el sistema 

es 

que corresponde a un sistema que tiene una respuesta de muestra unitaria no causal 

EJEMPLO 2.7.4 Si la respuesta de frecuencia de un sistema LSI es 

el sistema inverso es 

que tiene una respuesta muestral unitaria 

g(n) = (0.25)"u(n) + OS(0.25)"-'u(n - 1)

Problemas Resueltos 

 Problemas Resueltos

Respuesta frecuente

2.1 Sea h(n) la respuesta muestral unitaria de un sistema LSI. Encuentre la respuesta de frecuencia cuando

(a) h(n) = 6(n)+ 66(n - 1)+ 3S(n - 2)

1 n+2 (b) h(n) = (T) u(n -2).

(a) Este sistema tiene una respuesta de muestra unitaria de longitud finita. Por lo tanto, la respuesta de frecuencia es un polinomio

en ej", con los coeficientes del polinomio iguales a los valores de h(n):

~(ej")= 1 + 6e-I" + 3e-'jW

Esto puede mostrarse más formalmente escribiendo

Porque

entonces

ANÁLISIS DE FOURIER [CAP. 2

(6) Para el segundo sistema, la respuesta de frecuencia es

Cambiando los límites de la suma para que comience con n = 0, tenemos

Usando la serie geométrica, encontramos

2.2 Un filtro de media móvil de L-ésimo orden es un sistema lineal invariante por desplazamiento que, para una entrada x(n), produce la

producción

Encuentre la respuesta de frecuencia de este sistema.

Si la entrada al filtro de promedio móvil es x(n) = S(n), la respuesta, por definición, será la respuesta de la muestra unitaria,

h(n). Por lo tanto,

y

Usando la serie geométrica, tenemos

Factorizando un término e-j'L+')w/2 del numerador y un término e-~"/~ del denominador, tenemos

1 ,,,,, sen(L + 1142 H(eJW)= ~fle

pecado 0/2

2.3 La entrada a un sistema lineal invariante por desplazamiento es

Encuentre la salida si la respuesta de la muestra unitaria del sistema es

sen[(n -l)x/2] h(n) = 2

(n - 1)x

Este problema puede resolverse utilizando la propiedad de función propia de los sistemas LSI. Específicamente, como vimos en el Ejemplo 2.2.1, si la entrada a un sistema LSI es x(n) = cos(nq,), la respuesta será

~(n)= lH(eiw0)l cos(nwo + #dm))

CAP. 21 ANÁLISIS DE FOURIER 69

Por lo tanto, necesitamos encontrar la respuesta de frecuencia del sistema. En el Ejemplo 2.2.3, se demostró que la muestra unitaria

respuesta de un filtro de paso bajo ideal,

pecado ahora, hola@)= -

7 n

Como h(n)= 2hl (n - 1) con w, = 1712, se puede derivar una expresión para H(eJW) en términos de H,(ej") como sigue:

Por lo tanto,

Como IH(elw)(= 0 en w = 31714, la sinusoide en x(n) se filtra y la salida es simplemente

2.4 Encuentre la magnitud, la fase y el retardo de grupo de un sistema que tiene una respuesta de muestra unitaria

h(n) = S(n) - cd(n - yo)

donde ol es real.

La respuesta de frecuencia de este sistema es

Por lo tanto, la magnitud al cuadrado es

La fase, por el contrario, es

H[(eJW) gh(w)= tan-' ---- = tanp' a sin w

HR(eiw) 1 -crcosw

Finalmente, el retardo de grupo se puede encontrar diferenciando la fase (vea el problema 2.19). Alternativamente, podemos señalar que

debido a que este sistema es el inverso del considerado en el Ejemplo 2.2.2, la fase y el retardo de grupo son simplemente

el negativo de los encontrados en el ejemplo. Por lo tanto, tenemos

2.5 Un desfasador de 90" es un sistema con una respuesta de frecuencia

ANÁLISIS DE FOURIER [CAP. 2

Tenga en cuenta que la magnitud es constante para todo o, y la fase es -n/2 para 0 < o < n y n/2 para

-IT < w < 0. Encuentre la respuesta muestral unitaria de este sistema.

La respuesta de la muestra unitaria se puede encontrar por integración:

Por lo tanto, tenemos

impar

h(n) = yo nn

n incluso

que también se puede expresar como

filtros

2.6 Sea h(n) la respuesta de muestra unitaria de un filtro de paso bajo con una frecuencia de corte o,

¿Qué tipo de filtro tiene una respuesta de muestra unitaria g(n)= (- l)"h(n)?

Si se implementa un filtro con una respuesta muestral unitaria h(n) con una ecuación en diferencias de la forma

¿Cómo se debe modificar esta ecuación en diferencias para implementar el sistema que tiene una muestra unitaria?

respuesta g(n)= (- 1)" h(n)?

Dado que g(n) = (- l)"h(n), la respuesta de frecuencia G(eJU) está relacionada con la respuesta de frecuencia del paso bajo

filtro, H(eJU), como sigue:

Por lo tanto, G(ejU) se forma desplazando ~(ej") en frecuencia por 7r. Por lo tanto, si la banda de paso del filtro de paso bajo

es lo[ 5 w,, la banda de paso de G(ejU) será n - w, < Iwl n. Como resultado, se sigue que g(n) es la unidad

respuesta de muestra de un filtro de paso alto.

Si se puede realizar un filtro con una respuesta de muestra unitaria h(n) mediante la ecuación de diferencia dada en la Ec. (2.7). el

La respuesta de frecuencia del filtro es

H(eJw)= k=O

Multiplicando h(n) por (-1)"produce un sistema con una respuesta de frecuencia

CAP. 21 ANÁLISIS DE FOURIER

Porque eJkn= (-I)),

y la ecuación en diferencia se convierte en

Eso es. los coeficientes a(k) y b(k) fork impar son negados,

2.7 Sea H(eJm) la respuesta de frecuencia de un filtro de paso bajo ideal con una frecuencia de corte wc como se muestra en

la figura de abajo.

Suponga que la fase es lineal, #h(w) = -ahora. Determinar si es posible o no encontrar una entrada

x(n) y una frecuencia de corte w, < n que producirá la salida

Yo 1 n=0,1, ..., 20

= 0 de lo contrario

Si X(eJo) es la DTFT de x(n), la salida del filtro de paso bajo tendrá una DTFT

Por lo tanto, Y (do) debe ser igual a cero para w,. 5 lo(5 n. Sin embargo, la DTFT de y(n) es

que no es cero para w, p lo1 5 n. Por lo tanto, no hay valor para w, < n, y no hay entrada x(n) que genere

la salida dada y(n).

2.8 Sea h(n) la respuesta de muestra unitaria de un filtro de paso bajo ideal con una frecuencia de corte wc = n/4. Se muestra en la

la siguiente figura es un sistema lineal invariante por desplazamiento que se forma a partir de una cascada de un filtro de paso bajo y dos

moduladores. Encuentre la respuesta de frecuencia del sistema general que relaciona la entrada x(n) con la o salida y(n).

Hay dos formas que podemos usar para encontrar la respuesta de frecuencia de este sistema. La primera es señalar que debido a que

la entrada al filtro de paso bajo es (- I)"x(n), la salida del filtro de paso bajo es

ANÁLISIS DE FOURIER [CAP. 2

Por lo tanto.

Llevando el término (-1)" dentro de la sumatoria, y usando el hecho de que (-I)"-~ = (- tenemos

Por lo tanto, la respuesta de la muestra unitaria del sistema total es (- I)"h(n), y la respuesta de frecuencia es

10 de lo contrario

Otra forma de determinar la respuesta de frecuencia es encontrar la respuesta del sistema a una exponencial compleja,

x(n) = eln'". Modulando por (-1)" = e-inn produce la secuencia

que es la entrada al sistema LSI. Como u(n) es una exponencial compleja, la respuesta del sistema a v(n) es

se deduce que la respuesta de frecuencia de todo el sistema es H (d('"-"') como encontramos antes.

2.9 Si h(n) es la respuesta de muestra unitaria de un filtro de paso bajo ideal con una frecuencia de corte w, = n/4, encuentre la

respuesta de frecuencia del filtro que tiene una respuesta de muestra unitaria g(n) = h(2n).

Para encontrar la respuesta de frecuencia de este sistema. podemos resolver el problema de una de dos maneras. La primera es señalar que

porque la respuesta de muestra unitaria de un filtro de paso bajo ideal con una frecuencia de corte w,. = n/4 es

entonces

que es la respuesta de muestra unitaria de un filtro de paso bajo con una magnitud de 4 y una frecuencia de corte w = n/2. El

La segunda forma de trabajar este problema es encontrar la respuesta de frecuencia del sistema que tiene una respuesta de muestra unitaria.

g(n) = h(2n), dado que H(el'") es la respuesta en frecuencia de un sistema con una respuesta muestral unitaria h(n). Aunque

más difícil que el primer enfoque. esto dará una expresión general para la respuesta de frecuencia G(eJw) en términos

de H(ejw) que se puede aplicar a cualquier sistema. Para encontrar la respuesta de frecuencia, debemos evaluar la suma

usando la identidad

2 n par I +(-I)" = I 0 n impar

podemos escribir la respuesta de frecuencia como

CAP. 21 ANÁLISIS DE FOURIER

En términos de H(dw), el primer término se puede escribir como

mientras que el segundo término es

Con ~(ej~) la respuesta de frecuencia de un filtro de paso bajo con una frecuencia de corte w, = n/4, esto da el mismo resultado

como antes.

2.10 Considere el filtro de paso alto que tiene una frecuencia de corte w = 3n/4 como se muestra en la siguiente figura:

(a) Encuentre la respuesta de la muestra unitaria, h(n).

(h) Un nuevo sistema se define de modo que su respuesta muestral unitaria sea hl(n) = h(2n). Dibuje la frecuencia

respuesta, H I(ej"), de este sistema.

(a) La respuesta de la muestra unitaria se puede encontrar de dos maneras diferentes. La primera es usar la fórmula DTFT inversa y

realizar la integración. El segundo enfoque es usar la propiedad de modulación y notar que si

yo por lo[5 -

3r

cadera(eJW)= 4

0 de lo contrario

H(eJu) puede escribirse como

H (@) = HIp(eJ("-"'1

Por lo tanto, de la propiedad de modulación se sigue que

h(n) = eJn"hlp(n)= (-l)"hlp(n)

Con

tenemos

(6) La respuesta de frecuencia del sistema que tiene una respuesta de muestra unitaria h I (n) = h (2n) se puede encontrar evaluando

la transformada de Fourier en tiempo discreto suma directamente:

n=-00 n=-m n par

ANÁLISIS DE FOURIER [CAP.2

Sin embargo, un enfoque más fácil es notar que

que es un filtro de paso bajo con una frecuencia de corte de n/2 y una ganancia de f. En la figura se muestra un gráfico de H,(~J").

siguiente figura:

Interconexión de Sistemas

2.11 Los filtros ideales que tienen respuestas de frecuencia como se muestra en la siguiente figura están conectados en cascada.

Para una entrada arbitraria x(n), encuentre el rango de frecuencias que pueden estar presentes en la salida y(n). Repetir

para el caso en que los dos sistemas estén conectados en paralelo.

Si estos dos filtros están conectados en cascada, la respuesta de frecuencia de la cascada es

Por lo tanto, cualquier frecuencia en la salida, y(n), debe pasar por ambos filtros. Porque la banda de paso para Hl(ejW) es

Iwl > n/3, y la banda de paso para H2(eJU) es n/4 < Iwl < 3x14, la banda de paso para la cascada (las frecuencias para

que tanto I H I(eJ1')1 como I Hz(ejU)la son iguales a I) es

Con una conexión en paralelo, la respuesta de frecuencia general es

Por lo tanto, las frecuencias que están contenidas en la salida son aquellas que pasan por el filtro o

2.12 Considere la siguiente interconexión de sistemas lineales invariantes por desplazamiento:

CAP. 21 ANÁLISIS DE FOURIER

Encuentre la respuesta de frecuencia y la respuesta de muestra unitaria de este sistema.

Para encontrar la respuesta de la muestra unitaria, sea x(n) = S(n). La salida del sumador es entonces

Debido a que w(n) se ingresa a un sistema LSI con una respuesta de muestra unitaria h2(n),

sin(nn/2) donde hz(n) = - ~~(~jf~)~jlj~d~ eJnwdw= --- 2n ' I" -, 2n -,,Z nn = -

I""

Por lo tanto, la respuesta de la muestra unitaria de todo el sistema es

Para encontrar la respuesta de frecuencia, tenga en cuenta que

Por lo tanto, ~(ej")= w(~~")H:(~J"') = [I - e-j"]~

2.13 Considere la interconexión de sistemas LSI que se muestra en la siguiente figura:

--hzb)

x(n)L

- - hl(n) -

L

- L hdn) hdn) -

(a) Exprese la respuesta de frecuencia de todo el sistema en términos de H I(ej"), H2(ejw),FZ3(ejo) y

H4 (ejw).

(b) Encuentre la respuesta de frecuencia si

(a) Como h2(n) está en paralelo con la cascada de h3(n) y h4(n), la respuesta de frecuencia de la red en paralelo es

Con hl(n) estando en cascada con g(n), la respuesta de frecuencia general se convierte en

~(ej")= HI(eiW)[Hz(ei")+ H3(ejw)H4(eJW)1

ANÁLISIS DE FOURIER [CAP. 2

(b) Las respuestas de frecuencia de los sistemas en esta interconexión son

Por lo tanto,

2.14 Suponga que la respuesta de frecuencia de un sistema lineal invariante por desplazamiento es constante por tramos, como se muestra en

la siguiente figura:

Describa cómo se puede implementar este filtro como una conexión paralela de filtros de paso bajo.

Este filtro puede verse como la suma de un filtro de paso bajo, un filtro de paso de banda y un filtro de paso alto. Porque

Tanto un filtro de paso de banda como un filtro de paso alto se pueden sintetizar utilizando una conexión paralela de filtros de paso bajo.

puede proceder de la siguiente manera. Primero, ponemos un filtro de paso total H3(eJW)= A3 en paralelo con un filtro de paso bajo con un corte

frecuencia 02 y una ganancia de Az - A3. Esta red paralela tiene una respuesta de frecuencia

Para producir la magnitud correcta sobre la banda inferior, Iwl iwl, agregamos un tercer filtro de paso bajo en paralelo con el

otros dos. Este filtro tiene una frecuencia de corte de wl y una ganancia de A I - A2.

2.15 Dos sistemas lineales invariantes al desplazamiento están conectados en una red de retroalimentación como se ilustra en la siguiente figura.

Suponiendo que todo el sistema es estable, de modo que H(ej") existe, demuestre que la respuesta de frecuencia de

esta red de retroalimentación es . Y (ej") F (ei") J" - -- H(e ) - X(ejm) 1 -F(ej")G(ej")

Para analizar esta red, comenzamos por señalar que

CAP. 21 ANÁLISIS DE FOURIER

que, en el dominio de la frecuencia, se convierte en

W (el") = X(eJW)+ G ( e J " ) Y( e l W )

Porque y(ejw)= F(eJw)w(el")

entonces Y(elw)= F(ejw)[x(eJw)+ G ( e I w ) Y( e l w ) ]

Resolviendo para ~(ri")rendimientos

Por lo tanto, la respuesta de frecuencia es

La transformada de Fourier en tiempo discreto

2.16 El LCCDE describe un sistema lineal invariante por desplazamiento

Encuentre el valor de b para que IH(eJm)l sea igual a I en w = 0, y encuentre el punto de potencia del heno (es decir, el

frecuencia en la que I H(ejW)I2 es igual a la mitad de su valor máximo, que se produce en w = 0).

La respuesta de frecuencia del sistema descrito por esta ecuación en diferencia es

b2 bZ

Porque l~(ej")l~= - ( 1 -0.5e-jw)(1 -0.5ejw) 1.25 -cos w

IH(eJw)l será igual a 1 en o = 0 si

h2 -- - 1

1.25 - 1

Esto será cierto cuando b = f0.5.

Para encontrar el punto de media potencia, queremos encontrar la frecuencia para la cual

0.25

IH(~'")I~ = = 0.5 1 .25 -cos o

Esto ocurre cuando

cos o = 0,75

o o = 0,2317.

2.17 Considere el sistema definido por la ecuación en diferencias

donde a y b son reales, y la I < 1. Encuentra la relación entre a y h que debe existir si la frecuencia

respuesta es tener una magnitud constante para todo w, es decir,

IH(~~*)I = 1

ANÁLISIS DE FOURIER [CAP. 2

Suponiendo que se cumple esta relación, encuentre la salida del sistema cuando a = y

x(n) = (;)"u(n)

La respuesta de frecuencia del sistema LSI descrito por esta ecuación en diferencia es

La magnitud al cuadrado es

(b+ e-jo)(h+ eJ") 1 + h2+ 2b cos w IH(~'")I~ = - (1 -ae-JU)(l-aeju) I + a2 -2a cos w

Por tanto, se sigue que I H(e'")12 = 1 si y sólo si b = -a.

Con a = y h = -;, si x(n)= (i)"u(n),Y(ejU)está dada por

Usando el par DTFT

dado en la Tabla 2-1, y utilizando las propiedades de linealidad y retardo de la DTFT, tenemos

Lo que observamos de este ejemplo es que aunque I H(eJU)l= 1, la fase no lineal tiene un efecto significativo en

los valores de la secuencia de entrada.

2.18 Demuestre que el retardo de grupo de un sistema lineal invariante con desplazamiento con una respuesta de frecuencia H(ejw) puede ser

expresado como

HR(~~,)GR(dw) + H I(ejW)G(ejw)

th(~)= I H(ejw)I2

donde HR(eJw) y Hl(ejw) son las partes real e imaginaria de H(ejw), respectivamente, y GR(ejW) y

Gr(ejw) son las partes real e imaginaria de la DTFT de nh(n).

En términos de magnitud y fase, la respuesta de frecuencia es

Note que si tomamos el logaritmo de H(eJW), tenemos una expresión explícita para la fase

Derivando con respecto a esto, tenemos

Igualando las partes imaginarias de ambos lados de esta ecuación se obtiene

CAP. 21 ANÁLISIS DE FOURIER

si definimos

d

-H(eJ") = Hk(ei") + j ~;(ej") dw

donde HA(eJW) es la derivada de la parte real de H(eiw) y H;(ejW) es la derivada de la parte imaginaria, la

el retraso de grupo se puede escribir como

Multiplicando el numerador y el denominador por H*(eJw) = HR(eJW)-jHI(eJW) se obtiene

Finalmente, recuerda que si H (eJ") es la DTFT de h(n), la DTFT de g(n) = nh(n) es

donde GR(eJWj es la parte real de la DTFT de nh(n), y GI (elW) es la parte imaginaria. Por tanto, HA(eJW) = GI (elW)

y H;(~J") = -GR(eJW). Expresado en términos de GR(ejW) y GI(eJW), el retardo de grupo se convierte en

Tenga en cuenta que esta expresión para el retardo de grupo es conveniente para la evaluación digital, porque i ~ solo requiere calcular

la DTFT de h(n) y nh(n), y sin derivadas.

2.19 Encuentre el retardo de grupo para cada uno de los siguientes sistemas, donde a! es un número real:

(a) H l(ejw)= 1 - ae-jo

1 (b) H2(ejw) = 1 -me-Jw

1

(c) H3(ejw)= 1 -2a! cos 8e-jw +a!2e-j2w

(a) Para el primer sistema, la respuesta de frecuencia es

H, (eJ") = 1 -a cos w + ja sen w

Por lo tanto, la fase es un seno w

$1 (w) = tan-'

1 -acosw

Porque

el retraso del grupo es

d 1 a sen w r~(w)= = - dw I -a COEw

1 (1 - acosw)aco~w- (asinw)' Por lo tanto, rl(w) = -

1 + (-)2 (1 -(Y cos w)~

ANÁLISIS DE FOURIER [CAP. 2

que, después de la simplificación, se convierte en

(I-acos~)aco~w-(asinw)~ a2-acosw - q(w) = - - (1 -a cos w)~ + (a sen w)Z I +az-2acosw

Otra forma de resolver este problema es utilizar la expresión del retardo de grupo derivada de Rob. 2.18. Con

Hl(eJ") = 1 -acosw+ jasinw

vemos eso

HR(eJw)= 1 -a cos w Hl(eJw)= a sen w

Como la respuesta de la muestra unitaria es

h(n) = S(n) -aS(n - 1)

entonces g(n) = nh(n) = -a6(n -I)

y G(ejw)= -ae-jw = -a cos w + ja sin w

Por lo tanto, el retardo de grupo es

que es lo mismo que antes.

(b) Habiendo encontrado el retardo de grupo para Hl(ejW) = 1 -ae-J", podemos derivar fácilmente el retardo de grupo para H2(eJW),

que es el inverso de Hl(eJw):

Específicamente, porque

1 Hz(eJ") = -

Hz(eJ")

&(w) = -@I(w) y, por tanto,

(c) Para el último sistema, H3(eJw) puede factorizarse como sigue:

El retardo de grupo de H3(eJm) es, por tanto, la suma de los retardos de grupo de estos dos factores. Además, el grupo

el retraso de cada factor se puede encontrar directamente diferenciando la fase. Sin embargo. el retraso del grupo de

estos términos también se pueden encontrar en t2(w) en la parte (b) si usamos la propiedad de modulación de la DTFT. Específicamente,

recuerda que si X(ejw) es la DTFT de x(n), la DTFT de ejn0x(n) es

Por lo tanto, si el retardo de grupo de x(n) es ~(w), el retardo de grupo de ejdx(n) será r(w -8). En la parte (b), encontramos

que el retardo de grupo de H (ej") = 1/(I -cue-'") es

CAP. 21 ANÁLISIS DE FOURIER

Por tanto, de la propiedad de modulación se sigue que el retardo de grupo de H(ejw) = ]/(I -ae-~(~-O') es

y que el retardo de grupo de H(ejW) = 1/(1 - ae-j"u+e)) es

Por lo tanto, el retardo de grupo de H3(eJW) es la suma de estos:

2.20 Encuentre la DTFT de cada una de las siguientes secuencias:

(a) X I(n)= ($)"u(n + 3)

(b) xz(n)= CY" sen(nwo) u(n) 1 A;)" n = 0.2.4, . . . (c) x3(n) = de lo contrario

(a) Para la primera secuencia, la DTFT puede evaluarse directamente de la siguiente manera:

(b) La mejor manera de encontrar la DTFT de xz(n) es expresar la sinusoide como una suma de dos exponenciales complejas de la siguiente manera:

De manera similar, para el segundo término tenemos

Por lo tanto,

X2(eJW)= -

I [ 1 - (un pecado wo)e-jw

2j 1 -ae-j(w-"o) 1 - I -(hcos wo)e-jw + cr2e-Zjw

(c) Finalmente, para xj(n), tenemos

Por lo tanto,

82 ANÁLISIS DE FOURIER [CAP. 2

2.21 Debido a que la DTFT de la salida de un filtro invariante con desplazamiento lineal con respuesta de frecuencia H(ejw) es

donde x(ejw) es la DTFT de la entrada, se deduce que un sistema LSI no puede producir frecuencias en el

salida que no están presentes en la entrada. Por lo tanto, si un sistema introduce nuevas frecuencias. el sistema

debe ser no lineal y/o variable por turnos. Para cada uno de los siguientes sistemas, encuentre las frecuencias que son

presente en la salida cuando x(n) = cos(nwo):

(a) Con x(n) = cos(nmo), la salida del dispositivo de ley cuadrática es

y(n) = cos2(nw)

Usando la identidad trigonométrica

cos2 A = f + cos(2A)

resulta que

y(n) = + f cos(2nm)

Por tanto, aunque las únicas frecuencias presentes en la entrada son w = fwo. las frecuencias en la salida son

w = 0, f2mn. Debido a que este sistema no es lineal, crea frecuencias en la salida que no están en la entrada.

(b) Para el modulador, la salida es

Usando la identidad trigonométrica

2 cos A cos B = cos (A + B) + cos (A - B)

resulta que

y(n) = cos(nmo + 7)+ cos(mn -7)

Por lo tanto, las frecuencias en la salida son w = wo frj4, que son diferentes a las de la entrada. Esto es

porque el modulador es un sistema de cambio variable.

(c) El último sistema, llamado down-sampler, produce la salida

creando así frecuencias en la salida que no están presentes en la entrada. El down-sampler es un cambio variable

sistema.

Para cada uno de los siguientes pares de señales, x(n) e y(n), determine si hay o no una señal lineal.

sistema invariante por corrimiento que tiene la respuesta dada, y(n), a la entrada dada, x(n). Si tal sistema existe,

determinar si el sistema es único o no, y encontrar la respuesta de frecuencia de un sistema LSI con

el comportamiento deseado. Si no existe tal sistema LSI, explique por qué.

(4 x(n) = (i)"u(n), y(n) = (a)"u(n)

(b) x(n) = ejnnf4, y(n) = 0.5cj""/4

sin(nnf4) , y(n) - sin(nnf2) (c) x(n) = 7 nn

(4 x(n) = u(n), y(n) = 6(n)

CAP. 21 ANÁLISIS DE FOURIER

(a) Para el primer par de entrada-salida, tenemos

Como X(ejW) es distinto de cero para todo w, el sistema que produce la respuesta y(n) es único y viene dado por

(b) Para el segundo sistema, tenga en cuenta que la entrada es una exponencial compleja con una frecuencia w = n/4. Por lo tanto, si

el sistema es LSI, la salida debe ser una exponencial compleja de exactamente la misma frecuencia, es decir,

Y(n)= ~(~jW4 )ehn/4

Porque la salida es

y(n) = 0.5 ejnnI4

cualquier sistema LSI con

H ( mi J norte l 4 ) = 0.5

producirá la respuesta dada. Por lo tanto, el sistema no es único. Un posible sistema es el filtro de paso bajo

TT

H (eJ")=

de lo contrario

(c) Para el tercer sistema, recuerde que un filtro de paso bajo ideal con una frecuencia de corte w,. tiene una respuesta muestral unitaria

dado por (ver Ejemplo 2.2.3)

pecado no, h(n)= -

rn

Por lo tanto, la DTFT de la entrada x(n) es

TT

1 I4 -= qX(el") =

0 de lo contrario

y la DTFT de la salida y(n) es TT

Y reJ")=

' (0o de lo contrario

Dado que X(ejw)= 0 para Iwl n/4, si el sistema va a ser lineal e invariante frente al desplazamiento, Y (el") debe ser igual a cero

para lo1 > n/4 (un sistema LSI no puede producir nuevas frecuencias). Porque este no es el caso, ningún sistema LSI

producirá el par entrada-salida dado.

(d) Para el último sistema, tenemos x(n) = u(n) e y(n) = S(n). Por lo tanto,

y

Como en la parte (a), hay un sistema LSI único que produce este par de entrada-salida, y la respuesta de frecuencia de

este sistema es

2.23 Encuentra la DTFT de la secuencia de dos colas

ANÁLISIS DE FOURIER [CAP. 2

Tenga en cuenta que podemos escribir x(n) como la suma de una secuencia del lado izquierdo y una secuencia del lado derecho de la siguiente manera:

donde el último término se incluye para eliminar el término extra que se introduce en n = 0 por las dos secuencias exponenciales.

La DTFT del primer término es

y, usando la propiedad de inversión del tiempo, se sigue que la DTFT del segundo término es

1 Por lo tanto, IW - ( - 1 --

yo +--yo yo - le,w

2.24 Usar la ortogonalidad de las exponenciales complejas

para mostrar que x(n) se puede recuperar de X(eju) de la siguiente manera:

Dada una secuencia x(n), la DTFT está definida por

Para recuperar x(n) de X(eJm), es necesario "filtrar" todos los términos de la suma excepto uno (es decir, debemos aislar

un solo término en la suma). Esto se puede hacer multiplicando ambos lados de la ecuación por una exponencial compleja, elnw:

e integrando de -n a n,

Intercambiando el orden de la integral y la suma de la derecha da

Usando la ortogonalidad de las exponenciales complejas, se sigue que la integral es cero cuando k # n, y es igual

a 2n cuando k = n. Por lo tanto,

Dividir ambos lados por 2n da el resultado deseado.

CAP. 21 ANÁLISIS DE FOURIER

2.25 Encuentre la DTFT inversa de X(e1"') que se muestra en la siguiente figura:

X(eJU) t

Debido a que X(eJU) es una función constante por partes de w, encontrar la DTFT inversa puede lograrse fácilmente mediante

integración. Usando la DTFT inversa, tenemos

Reordenando los términos, tenemos

cual es el resultado deseado.

Es interesante notar que x(n) se expresa como la diferencia de dos secuencias, siendo la primera un ideal

filtro de paso bajo con una frecuencia de corte de 3x14, y el segundo un filtro de paso bajo ideal con una frecuencia de corte de

n/4. Esto es consecuencia del hecho de que X(ei"') puede expresarse como

3rc

donde X,(eJ")= I Iwl < q

0 de lo contrario

rc

X2(cJW)= 1 Iwl < q y

0 de lo contrario

Otra forma de evaluar la DTFT inversa es observar que x(eiw) puede escribirse como

X(eJ")= X~(~J'"'+?)+ X, e~'co-?) > -('

donde Xz(ejw) es el filtro de paso bajo ideal definido anteriormente. Por lo tanto, X(eJU') puede verse como un filtro de paso bajo modulado:

sin(na/4) Con x2(n) = -

nrc

x(n) también se puede escribir como

Se puede demostrar que esto es equivalente a la representación anterior para x(n) usando la identidad trigonométrica

2 sen A sen B = sen (A + B) + sen (A -B)

86 ANÁLISIS DE FOURIER [CAP. 2

2.26 Encuentre la DTFT inversa de x(~J")= cos2 w.

Recuerde que la DTFT de una muestra unitaria retardada es una exponencial compleja:

DTFT -inow S(n -no) e

Por lo tanto, la DTFT inversa de X(ejW)= cos2w se puede encontrar fácilmente si la expandimos en términos de exponente complejo. Así, se sigue que x(n) es

x(n) = iS(n)+ as(n + 2) + fS(n - 2)

2.27 Si h(n) es la respuesta muestral unitaria de un sistema real y causal lineal invariante con el desplazamiento, demuestre que el sistema

está completamente especificado por la parte real de su respuesta de frecuencia:

En otras palabras, demuestre que H(eJW) puede recuperarse únicamente de su parte real.

Recuerde de las propiedades de simetría de la DTFT que si h(n) es real, H(el") es simétrica conjugada. Por lo tanto, si

H(eJw) se escribe en términos de sus partes real e imaginaria,

entonces la parte real, HR(ei"), es la DTFT de la parte par de h(n):

Por lo tanto, dado HR(eJW), o h,(n), la pregunta es cómo recuperar h(n). Nótese que si h(n) es causal, h(n) = 0 para

n < 0, y

ih(n) n > 0

n = O

kh(-n) norte 4 0

Como resultado, h(n) puede recuperarse de h,(n) de la siguiente manera:

Si h(n) es real y causal, y si

HR(el") = ~e{~(eJ")j = 1 + a cos 2 0

encontrar h(n).

Porque la parte real de H(eJw) es

~~(ej~) = 1 + a cos 2w = I + faeJ2"+ ;aeFizw

la parte par de h(n), que es la DTFT inversa de HR(eJw), es

h,(n) = 6(n)+ iaS(n + 2) + $d(n - 2)

Siendo h(n) una secuencia causal, se sigue de los resultados del Prob. 2.27 que

lo que da

CAP. 21 ANÁLISIS DE FOURIER

Propiedades DTFT

2.29 Demuestre que si x(ejw) es real y par, x(n) es real y par.

Para x(n) tenemos

Si ~(ej") es real e impar, entonces X(ej'") sin(nw) es real e impar. Por lo tanto, cuando se integra de -n ton, la integral

es cero Por lo tanto, x(n) puede escribirse como

y se sigue que x(n) es real. Finalmente, como X(ejW) cos(nw) es real y par, x(n) es real y par, es decir,

2.30 Demuestre el teorema de convolución.

Hay varias formas de probar el teorema de la convolución. Una forma es mediante una manipulación directa de la DTFT.

suma. Específicamente, si y(n) = h(n)* .u(n),

y la DTFT de y(n) es

Tenga en cuenta que la expresión entre paréntesis es la DTFT de x(n -1). Usando la propiedad de retardo de la DTFT, esto es igual a

x(ejW)e-J'", y el lado derecho de esta ecuación se convierte en

Factorizando X(eJW) de la suma, que no no dependemos de yo, tenemos

lo que prueba el teorema.

Otra forma de probar el teorema de convolución es considerar la siguiente cascada de dos sistemas LSI, uno

con una respuesta muestral unitaria de h(n) y la otra con una respuesta muestral unitaria de x(n):

Si la entrada a esta cascada es una exponencial compleja, ej"", la salida del primer sistema es H(ejw)ejnw. Debido a que esto

exponencial compleja es la entrada al segundo sistema, la salida es H(ej")X(ej")eJn". Por lo tanto, H(ej")X(ejw)

es la respuesta de frecuencia de la cascada, y debido a que la respuesta de muestra unitaria de la cascada es la convolución

h(n)* x(n), tenemos el par DTFT

h(n) * x(n) D&T H (ejw)x(dw)

que establece el teorema de convolución.

88 ANÁLISIS DE FOURIER [CAP. 2

2.31 Deduzca la propiedad de muestreo ascendente de la DTFT, que establece que si x (ej") es la DTFT de x(n), la DTFT de

n =O,&L,f2L, ... y(n) =

de lo contrario

De la definición de la DTFT, tenemos

Como y(n) es igual a cero excepto cuando n es un múltiplo entero de L,

n-m ,,=-m

Así, Y(eJW) se forma escalando X(eJW) en frecuencia.

2.32 Encuentre la DTFT inversa de

1 I" - X(e ) -,-;e-j,h

Para este problema, el enfoque directo de realizar la integración

no es fácil. Sin embargo, un enfoque simple es recordar que la DTFT inversa de

es y(n) = (f)"u(n)

y notar que ~(ej") está relacionado con X(eju) escalando en frecuencia,

~(ej")= Y (eJIOw1

Por lo tanto, se sigue de la propiedad de muestreo ascendente en el problema. 2.3 1 que

de lo contrario 1O

En otras palabras, la secuencia x(n) se forma insertando nueve ceros entre cada valor de y(n).

2.33 Sea x(n) una secuencia con una DTFT ~(e;"). Para cada una de las siguientes secuencias que se forman a partir de

x(n), expresa la DTFT en términos de X(eJW):

(a) x*(-n>

(b) x(n) * x*(-n)

c) x(2n + 1)

CAP. 21 ANÁLISIS DE FOURIER

(a) La DTFT de x*(-n) es

Llevando el conjugado afuera, tenemos

lo que conduce al par DTFT

x*(-n) Dgx*(ejw)

(b) Para y(n) = x(n) * x*(-n), tenga en cuenta que debido a que y(n) es la convolución de dos secuencias, la DTFT de y(n) es la

producto de las DTFT de x(n) y x*(-n). Como se muestra en la parte (a), la DTFT de x*(-n) es X*(ejW). Por lo tanto,

tenemos el par DTFT

x(n) * x*(-n) Ds~(ej")~*(e'")= 1~(ej")1~

(c) Para x(2n + 1) tenemos

DTFT(x(2n + I)) = 2r(2n + 1)e-In" = xx(n)e-jnY

n=-m n impar

Para evaluar esta suma, un "truco" es usar la identidad

2 n impar 1 - = 0 n par

Esto nos permite escribir la DTFT de la siguiente manera:

metro

DTFT(x(2n + 1)) = x(n)e-jn" = x[I -(-lr]x(n)e-jnw

n impar n=-m

Porque la primera suma es simplemente X(eJU), y la segunda es la DTFT de la señal modulada

entonces DTFT(x(2n + 1)) = f [x(eiw) -x(eicw-") )I

2.34 Sea x(n) la secuencia

que tiene un DTFT

~(ej")= xR(ej") + j~, (ej)

donde xR(ejw) y xl(ejw) son la parte real y la parte imaginaria de x(ejW), respectivamente. Encuentra el

secuencia y(n) que tiene una DTFT dada por

La clave para resolver este problema es recordar que si x(n) es real, y si X(eJW) se escribe en términos de su real y

partes imaginarias, XR(ejw) es la DTFT de la parte par de x(n), y Xl(eJW) es la DTFT de la parte impar:

x,(n> = [x(n) + x(-n)] DBxr(eiw)

x&) = f [x(n) -x(-n)]

DTFT.

IXl(ejw)

ANÁLISIS DE FOURIER [CAP. 2

Por lo tanto, la DTFT de -jx,(n) es Xl(ei"),

y la DTFT de jxe(n + 2) es

DTF. jxe(n + 2) c-T jXR(ejW)ejzW

Así, ixe(n + 2) -jx,(n) D& y(ejW)= X,(eJW)+ jXR(eiW)eJh

y se sigue que

y(n) = jxJn + 2) -jx&)

Finalmente, con xe(n) y x,(n) como se tabula a continuación.

se deduce que y(n), que se forma a partir de estas dos secuencias, es como se muestra a continuación:

2.35 Sea x(n ) la secuencia

Evalúe las siguientes cantidades sin encontrar explícitamente X(eJo):

(4x(ejo)lo=O

(b) 9Mw)

(c) x(eJo)dw

(4x(ejo)lo=r

(e) IX(ejw)l2d~

(a) Debido a que la DTFT de x(n) es ca

x(ejW)= )7 x(n)e-jnw

n=-m

tenga en cuenta que si evaluamos X (ejW) en w = 0, tenemos

que es simplemente la suma de los valores de x(n). Por lo tanto, para la sucesión dada se sigue que

(b) Para evaluar la fase, tenga en cuenta que debido a que x(n) es real y par, X(eJW) es real y par y, por lo tanto, la fase

es igual a cero o n para todo o.

CAP. 21 ANÁLISIS DE FOURIER

(c) De la DTFT inversa,

tenga en cuenta que cuando n = 0:

x(0) = -/' X(elY)dw 2n -,

Por tanto, se sigue que [:x(eM)do = 2nx(0) = 6n

(d) Evaluando la DTFT de x(n) en o = n, tenemos

que, para los valores dados de x(n), se evalúa como

(e) Por el teorema de Parseval, sabemos que

w

Por lo tanto, ll ~x(e~~)l'do = 271 lr(n)12 = 3871

n=-w

2.36 El centro de gravedad de una sucesión x(n) está definido por

y se utiliza como una medida del tiempo de retardo de una secuencia. Encuentre una expresión para c en términos de la DTFT

de x(n), y encuentre el valor de c para la secuencia x(n) que tiene una DTFT como se muestra en la figura a continuación.

Para encontrar el valor de c en términos de X(eJW), primero tenga en cuenta que el denominador es simplemente el valor de X(eJo) evaluado en

o = O: metro

Para el numerador, recuerde el par DTFT

nx(n) "Wj d ~ ~ m , hacer

ANÁLISIS DE FOURIER [CAP.2

Por lo tanto,

y c puede evaluarse en términos de X(eJm) como sigue:

Para la DTFT que se da, vemos que

X(eJm)l,,o = 1

y

L

Por lo tanto, C= -

norte

2.37 Para la secuencia x(n) graficada en la siguiente figura,

evaluar la integral

Esta integra l es fácil de evaluar si usamos el teorema de Parseval

y la propiedad derivada

Específicamente, tenemos

Aplicaciones

2.38 Un sistema lineal invariante por desplazamiento tiene una respuesta de frecuencia

1 H(ejw) = elo

1.1 +cosw

Encuentre un LCCDE que relacione la entrada con la salida.

CAP. 21 ANÁLISIS DE FOURIER 93

Para convertir H(eJw) en una ecuación en diferencias, primero debemos expresar H(eJW) en términos de exponenciales complejas.

Desarrollando el coseno en una suma de dos exponenciales complejas, tenemos

Multiplicar numerador y denominador por 2e-Jwgives

Multiplicando en cruz, tenemos

[I + 2.2e-i'u + e-2i"]~(eJ")= 2X(elw)

lo que lleva a la siguiente ecuación en diferencias cuando tomamos la DTFT inversa de cada término:

y(n) + 2.2y(n -I) + y(n - 2) = 2x(n)

2.39 Encuentre la respuesta de frecuencia de un sistema lineal invariante por desplazamiento cuya entrada y salida satisfacen la diferencia

ecuación

y(n) -0.5y(n - 1) = x(n) + 2x(n -I) +x(n -2)

Para encontrar la respuesta de frecuencia, comenzamos por encontrar la DTFT de cada término en la ecuación de diferencia

(I - OSe-j")Y(eJ") = (1 + 2e-1" + e-~'")x(eJ~)

Porque ~(ej")= ~(eJ")/X(ej").tenemos

2.40 Escriba una ecuación en diferencias para implementar un sistema con respuesta en frecuencia

Con

después de multiplicar en cruz, tenemos

[I + 0.5e-iw + 0.75e-zJ"]~(ei")= [l - 05-jw +e-3~"]~(eJ")

Tomando la DTFT inversa de cada término se obtiene la ecuación en diferencias deseada

y(n) +0.5y(n - 1 )+ 0.75y(n - 2) = x(n) -0.5x(n - 1) +x(n -3)

2.41 Encuentre una ecuación en diferencias para realizar un sistema lineal invariante con desplazamiento que tenga una respuesta de frecuencia

H(eJW)= bronceado w

Para encontrar una ecuación en diferencias para H(ejW), primero debemos expresar tan w en términos de exponenciales complejas:

pecado w yo ej" - e-I"

tanw= ---

cos w j elw + e-Jw

Con H(ejw)= Y(ejw)/X(ej") tenemos, después de multiplicar en cruz.

jlej" +e-j"]~(ej") = [ei" - e-j"]~(ej")

Transformando inversamente, obtenemos la siguiente ecuación en diferencias:

jy(n + 1) + jy(n - 1) = x(n + 1 ) -x(n - 1)

ANÁLISIS DE FOURIER [CAP. 2

Introduciendo un retardo y dividiendo por j, esta ecuación en diferencias se puede escribir en la forma más estándar

2.42 Encuentre una ecuación en diferencias para implementar un filtro que tenga una respuesta de muestra unitaria

Para encontrar una ecuación en diferencias para este sistema, primero debemos encontrar la respuesta de frecuencia H (elw). Expresando h(n) en

términos de exponenciales complejas,

se deduce que la respuesta de frecuencia es

Por lo tanto, la ecuación en diferencias para este sistema es

2.43 Un sistema con entrada x(n) y salida y(n) se describe mediante el siguiente conjunto de constantes lineales acopladas

ecuaciones de diferencias de coeficientes:

Encuentre una sola ecuación en diferencia de coeficiente constante lineal que describa este sistema, y encuentre la

respuesta de frecuencia H (elW).

Para encontrar la respuesta de frecuencia para este sistema de ecuaciones en diferencias, primero expresamos cada ecuación en la frecuencia

dominio:

Usando las dos últimas ecuaciones para expresar V(eJW) en términos de X(eJW), tenemos

Sustituyendo esta expresión por V(eJW) en la primera ecuación y resolviendo para Y(eJW) da

CAP. 21 ANÁLISIS DE FOURIER

Por lo tanto, la respuesta de frecuencia es

Multiplicando en cruz, tenemos

~(~iw)[l -ie-iw + ie-j2w] = x(~I~)[~-I"+ qe-2i" + ze-3iw]

y tomando la DTFT inversa de cada término se obtiene la ecuación en diferencias para el sistema:

y(n) -iy(n -I) + iy(n - 2) =x(n - I) + qx(n - 2) +2x(n - 3)

2.44 Un sistema lineal invariante con el desplazamiento con entrada x(n) y salida v(n) se describe mediante la ecuación en diferencias

Este sistema está conectado en cascada con otro sistema con entrada v(n) y salida y(n) que se describe mediante el

ecuación diferencial

y(n)=l ,Y(n-1) + 0)

¿Qué valor de cr garantizará que y(n) = x(n)?

Sustituyendo la primera ecuación en la segunda, obtenemos una única ecuación en diferencias que describe el sistema en su conjunto.

eso es,

y(n) = y(n - 1) +x(n)+ax(n - 1)

Tomando la DTFT de ambos lados de la ecuación, tenemos

y(ejw)= je-j"~(e~w) + x(~J") +ae-~w~(ej")

Si y(n) =x(n), Y(eiU) = X(eIu),y es claro que esto será cierto si y sólo si a = -4.

2.45 Encuentre la entrada x(n) que producirá una respuesta, y(n) =6(n),para un sistema descrito por LCCDE

Este problema se resuelve fácilmente si expresamos esta ecuación en diferencias en el dominio de la frecuencia. Específicamente, tenemos

y (,jw) -ie-iwy (,iw) = ~(~jw) - !e-ih~(e"JJ)

Si queremos que la salida sea y(n) =S(n), Y (ejw) = 1, y tenemos

Resolviendo para X(el") da

Para encontrar la DTFT inversa de X(ei"), recuerda que

Por lo tanto, la DTFT inversa de

yo" - 1

W(e) - 1 - Le-j2",

8

es la seuencia

w(n)= (y" n=0,2,4, ... en caso contrario

y x(n) está dada por

ANÁLISIS DE FOURIER [CAP. 2

Problemas complementarios

Respuesta frecuente

Considere un sistema lineal invariante con desplazamiento con una respuesta de muestra unitaria

h(n) = 6(n)+ 6(n - 1)

Encuentre la salida del sistema cuando la entrada es

Si la respuesta de la muestra unitaria de un sistema lineal invariante por desplazamiento es

h(n) = anu(n)

con la1 < I, encuentre la respuesta del sistema a la entrada x(n) = I. Repita para x(n) = (-1)".

Encuentre la respuesta de frecuencia del sistema que tiene una respuesta de muestra unitaria

(?(ahora) o 5 n 5 N - 1

h(n)= de lo contrario

La entrada a un sistema lineal invariante por desplazamiento es

Encuentre la salida cuando la respuesta de la muestra unitaria es

La entrada a un sistema invariante de desplazamiento lineal i s

x(n) = n(i)"u(n)

y la salida es

y(n) = (;)"-'u(n - 2) - (f)n-3 u(n -3)

Encuentre la respuesta de frecuencia ~(ej,).

Encuentre la respuesta de frecuencia del sistema descrito por el LCCDE

~(n) = iy(n - 10) +x(n) + js(n - 10)

Encuentre el retardo de grupo del sistema que tiene una respuesta de frecuencia

filtros

2.53 ¿Cuál es la respuesta de muestra unitaria de un filtro supresor de banda ideal con una frecuencia de corte inferior de o, y una frecuencia de corte superior

frecuencia de w?

2.54 Si h(n) es la respuesta de muestra unitaria de un filtro de paso bajo ideal con una ganancia de uno y una frecuencia de corte w = n/8,

¿Qué es g(n) = cos(nn/2)h(n)?

CAP. 21 ANÁLISIS DE FOURIER

La interconexión de sistemas

255 ¿Qué tipo de filtro tiene una respuesta de muestra unitaria?

2.56 ¿Cuál es la magnitud de la respuesta de frecuencia de la cascada de los siguientes dos sistemas?

La 'Ikansform' de Fourier en tiempo discreto

2.57 Encuentra la DTFT de la secuencia

x(n) = más

2.58 Para cada uno de los siguientes sistemas, encuentre las frecuencias que están presentes en la salida cuando la DTFT de la entrada

x(n) es

2.59 Sea x(n) = ejnnI4u(n) y y(n) = 0.5ejn"/4u(n). Determine si existe o no un sistema lineal invariante por desplazamiento

que tiene la respuesta, y(n), a la entrada x(n). Si tal sistema existe, determine si el sistema es único o no.

y encuentre la respuesta de frecuencia de un sistema LSI con el comportamiento deseado. Si no existe tal sistema LSI, explique por qué.

2.60 Encuentre la DTFT inversa de X(ejo) ilustrada en la siguiente figura.

2.61 Encuentre la DTFT inversa de X(eJW) ilustrada en la siguiente figura.

2.62 Encuentre la DTFT inversa de X(ejo) = cos 2w + j sen a.

2.63 Encuentre la DTFT inversa de

yo0 de lo contrario

ANÁLISIS DE FOURIER [CAP. 2

2.64 Encuentre la DTFT de

2.65 Si x(n) es real y causal, y

encontrar x(n).

Propiedades DTFT

2.66 Sea x(n) una secuencia con una DTFT X(ejw). Para cada una de las siguientes secuencias que están relacionadas con x(n), exprese

la DTFT en términos de X(ejW):

(4x*(n)

(h) x(n)-x(n-2)

(c)x(2n)

(d) x(n)* x(n -I)

2.67 Si la DTFT de x(n)= (i)"u(n+ 2)es X(ejW), encuentre la secuencia que tiene una DTFT dada por Y (ejw)= X(ejzo),

2.68 Sea x(n) la secuencia

x(n)= 26(n +3) - 26(n + I) +6(n -I) + 36(n -2)

Si la DTFT de x(n) se expresa en términos de sus partes real e imaginaria de la siguiente manera,

encontrar la sucesión y(n) que tiene una DTFT dada por

2.69 La DTFT de una sucesión x(n)es

3 JW -

X(e) - (1 - 0.Xe-jw)5

evaluar la suma

2.70 La DTFT de una sucesión .r(n)es

x(eJW)=cos3(3w)

evaluar la suma

2.71 Sean C:-,x(n) = A y x:-, h(n)= B. Si y(n)= h(n)* x(n), ¿es cierto que Cz-, y(n) ) = A. B?

2.72 Evalúe la siguiente integral:

[yo, yo

dw 1 -0.3e-jm

2.73 Usando el centro de gravedad (vea el problema 2.36), encuentre el tiempo de retraso de la secuencia

x(n)=anu(n)

-

CAP. 21 ANÁLISIS DE FOURIER

Aplicaciones de la DTFT

2.74 Un sistema causal lineal invariante con el desplazamiento se define mediante la ecuación en diferencias

2y(n)-y(n-2)=x(n-1) +3x(n-2) +2x(n-3)

Encuentre la respuesta de frecuencia, H (e'").

2.75 La respuesta de frecuencia de un sistema lineal invariante por corrimiento es

I H(eJW)= elw2 + e-2iw

Encuentre un LCCDE que relacione la entrada con la salida.

2.76 Encuentre el inverso del sistema que tiene una respuesta muestral unitaria h(n) = n(-k)"u(n -3).

Respuestas a problemas complementarios

1 yo

y(n) = y y(n) = -. 1 -a yo +a

(a) y(n) = $x(n). (b) y(n) = h~~ej""/~.

pecado(nwl) . h(n) = hl(n) +hz(n) donde hl(n) = ---1s un filtro de paso bajo ideal con una frecuencia de corte de wl, y

sin(nw) nw~ h2(n) = &(n)--es un filtro de paso alto ideal con una frecuencia de corte de w. nwz

Un filtro de paso de banda con una frecuencia de corte inferior de wl = 3n/8, una frecuencia de corte superior de wz = 5~/8 y una ganancia

de la mitad

Un filtro de paso alto con una frecuencia de corte w, = ~/3.

1 H (ejW)l= 1 para Iwl z 5 y I H (elW)l= 0 en caso contrario.

100 ANÁLISIS DE FOURIER [CAP.2

2n norte 5n 2n

(a) Iwl < -. (b) - < lo1 < -. (c) lo1 c -. 3 6 6 3

Único, h(n) = ;6(n).

n La DTFT es constante con una amplitud de a para lo1 < -, y decrece linealmente a cero en w = zt-.

3n

4 4

n = -4, -2.0,2,. .., y(n) =

de lo contrario

Comenzando con el índice n = -3, los valores de secuencia son [I, $, i,-i, -2. i. g, yo, -yo].

3 .s5.

Sí.

Capítulo 3. Muestreo 

 

3.1 Introducción 

 La mayoría de las señales de tiempo discreto provienen del muestreo de una señal de tiempo continuo, como señales de voz y audio, señales de radar y datos de sonar, y señales sísmicas y biológicas. El proceso de convertir estas señales en formato digital. se llama conversión de analógico a digital (AID). El proceso inverso de reconstruir una señal analógica a partir de su muestras se conoce como conversión de digital a analógico (D/A). Este capítulo examina los temas relacionados con A/D y Conversión D/A. Fundamental para esta discusión es el teorema de muestreo, que da condiciones precisas bajo que una señal analógica puede representarse de forma única en términos de sus muestras.

3.2 Conversión de analógico a digital 

 Un convertidor A/D transforma una señal analógica en una secuencia digital. La entrada al convertidor A/D, x,(t), es una función de valor real de una variable continua, t. Así, para cada valor de t, la función x,(t) puede ser cualquier Número Real. La salida del A/D es un flujo de bits que corresponde a una secuencia de tiempo discreto, x(n), con un amplitud que se cuantifica, para cada valor de n, a uno de un número finito de valores posibles. los componentes de un convertidor A/D se muestran en la Fig. 3-1. El primero es el muestreador, que a veces se denomina convertidor continuo a discreto (CP) o convertidor AlD ideal. El muestreador convierte la señal de tiempo continuo x,(t) en una secuencia de tiempo discreto x(n) extrayendo los valores de .u,(r) en múltiplos enteros del período de muestreo, T,

Debido a que las muestras x,(nTs) tienen un rango continuo de posibles amplitudes, el segundo componente del A/D convertidor es el cuantificador, que mapea la amplitud continua en un conjunto discreto de amplitudes. por un uniforme cuantificador, el proceso de cuantificación se define por el número de bits y el intervalo de cuantificación A. El último El componente es el codificador, que toma la señal digital i(n) y produce una secuencia de palabras codificadas binarias,

Figura 3-1. Los componentes de un convertidor de analógico a digital.

3.2.1 Muestreo periódico 

Por lo general, las señales de tiempo discreto se forman mediante el muestreo periódico de una señal de tiempo continuo

El espaciamiento de muestreo T, es el período de muestreo, yf, = I/T, es la frecuencia de muestreo en muestras por segundo. Una forma conveniente de ver este proceso de muestreo se ilustra en la figura 3-2(a). Primero, la señal de tiempo continuo es multiplicado por una secuencia periódica de impulsos, 

para formar la señal muestreada 

Luego, la señal muestreada se convierte en una señal de tiempo discreto al mapear los impulsos que están espaciados en el tiempo. por Ts en una secuencia x(n) donde los valores de la muestra están indexados por la variable entera n: 

Este proceso se ilustra en la Fig. 3-2(b)  

Figura 3-2. Conversión continua a discreta. (a) Un modelo que consiste en multiplicar x,(I) por una secuencia de impulsos seguido de un sistema que convierte los impulsos en muestras. (b) Un ejemplo que ilustra la proceso de conversión.

El efecto del convertidor C/D puede analizarse en el dominio de la frecuencia de la siguiente manera. Porque el Fourier transformada de 6(t -nTs) es e-JnnTs, la transformada de Fourier de la señal muestreada x,(t) es 

Otra expresión para Xs(jO) sigue al notar que la transformada de Fourier de s,(t) es 

donde 9, = 2n/T, es la frecuencia de muestreo en radianes por segundo. Por lo tanto,

Finalmente, la transformada de Fourier en tiempo discreto de x(n) es

Comparando la Ec. (3.3) con la ecuación. (3.2), se sigue que
 

Por lo tanto, X(eJW) es una versión escalada en frecuencia de X,(jQ), con la escala definida por 

Esta escala, que hace que x(~J") sea periódica con un período de 2n, es consecuencia de la escala temporal que se produce cuando x,(t ) se convierte en x(n). 

EJEMPLO 3.2.1 Suponga que xa(t) tiene un límite de banda estricto, de modo que Xa(jQ)= 0 para (RJ> Ro, como se muestra en la siguiente figura. 

Si xa(t) se muestrea con una frecuencia de muestreo Q, 2 2Q0, la transformada de Fourier de ~,~(t) se forma replicando periódicamente X,(jQ) como se ilustra en la siguiente figura. 

Sin embargo, si R, < 2R0, los espectros corridos X,,(jR -jkQ,) se superponen, y cuando estos espectros se suman para formar X,(jQ), el resultado es como se muestra en la siguiente figura.

Esta superposición de componentes espectrales se denomina aliasing. Cuando ocurre el aliasing, se completa el contenido de frecuencia de xa(t), y X,(jQ) no se puede recuperar de X,v(jQ). Como se ilustra en el Ejemplo 3.2.1, si x,(t) está estrictamente limitada en banda, de modo que la frecuencia más alta en x,(t) es Qo, y si la frecuencia de muestreo es superior a 2Q0, 

 no se produce aliasing, y x,(t) puede recuperarse únicamente de sus muestras xa(nTv) con un filtro de paso bajo. El siguiente es una declaración del famoso teorema de muestreo de Nyquist:Teorema de muestreo: si x,(t) está estrictamente limitado en banda, 

entonces x,(t) puede recuperarse únicamente de sus muestras x,(nT,) si 

La frecuencia Q0 se denomina frecuencia de Nyquist, y la frecuencia mínima de muestreo, Q, = 2'20, se denomina la tasa de Nyquist Debido a que las señales que se encuentran en los sistemas físicos nunca estarán estrictamente limitadas en banda, normalmente se usa un filtro antialiasing analógico para filtrar la señal antes del muestreo a fin de minimizar la cantidad de energía. por encima de la frecuencia de Nyquist y para reducir la cantidad de solapamiento que se produce en el convertidor AID.

3.2.2 Cuantización y codificación 

 Un cuantificador es un sistema no lineal y no invertible que transforma una secuencia de entrada x(n) que tiene un rango de amplitudes en una secuencia para la cual cada valor de x(n) asume uno de un número finito de posibles valores. Esta operación se denota por ,W) = Qlx(n)l El cuantificador tiene L + I niveles de decisión XI, xl, . . . . x~+[que dividen el rango de amplitud para x(n) en L intervalos 

Para una entrada x(n) que cae dentro del intervalo lk, el cuantificador asigna un valor dentro de este intervalo, &, tox(n). Este

El proceso se ilustra en la figura 3-3.

Figura 3-3. Un cuantificador con nueve niveles de decisión que divide las amplitudes de entrada en ocho intervalos de cuantificación y ocho posibles salidas de cuantificador. ir 

Los cuantificadores pueden tener niveles de cuantificación que están espaciados de manera uniforme o no uniforme. Cuando los intervalos de cuantificación están uniformemente espaciados,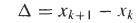 

A se denomina tamaño de paso de cuantificación o resolución del cuantificador, y se dice que el cuantificador es uniforme. o cuantificador lineal.' El número de niveles en un cuantificador es generalmente de la forma 

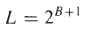
para hacer el uso más eficiente de una palabra de código binario de (B + 1) bits. Un cuantificador uniforme de 3 bits en el que el la salida del cuantificador se redondea al nivel de cuantificación más cercano, como se ilustra en la figura 3-4. Con L = 2'" cuantización niveles y un tamaño de paso A, el rango del cuantificador es 

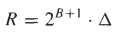
Por lo tanto, si la entrada del cuantificador está acotada, 

l*v(n)l5 Xmáx.

El rango de posibles valores de entrada puede cubrirse con un tamaño de paso 

Con redondeo, el error de cuantización 

En algunas aplicaciones, como la codificación de voz, los niveles del cuantificador son adaptativos (es decir, cambian con el tiempo). 

estará delimitado por 

Sin embargo, si (x(n)l excede X,,,, entonces x(n) se recortará y el error de cuantificación podría ser muy grande 

Figura 3-4. Un cuantificador uniforme de 3 bits.

En la figura 3-5 se presenta un modelo útil para el proceso de cuantificación. Aquí, el error de cuantificación se asume ser una fuente de ruido aditivo. Debido a que el error de cuantificación generalmente no se conoce, el error de cuantificación es descrito estadísticamente. Generalmente se supone que e(n) es una secuencia de variables aleatorias donde 

I. Las estadísticas de e(n) no cambian con el tiempo (el ruido de cuantificación es un proceso aleatorio estacionario).

2. El ruido de cuantificación e(n) es una secuencia de variables aleatorias no correlacionadas.

3. El ruido de cuantificación e(n) no está correlacionado con la entrada del cuantificador x(n).

4. La función de densidad de probabilidad de e(n) se distribuye uniformemente en el rango de valores del error de cuantificación.

Aunque es fácil encontrar casos en los que estos supuestos no se cumplen (por ejemplo, si x(n) es una constante), son generalmente válido para señales de variación rápida con cuantificación fina (A pequeña).

Figura 3-5. Un modelo de ruido de cuantización.

Con el redondeo, el ruido de cuantificación se distribuye uniformemente en el intervalo [-A/2, A/2], y el

la potencia del ruido de cuantificación (la varianza) es 

Con un tamaño de paso 

 y una potencia de señal ?:, la relación señal-ruido de cuantificación, en decibelios (dB), es

Por tanto, la relación señal/ruido de cuantificación aumenta aproximadamente 6 dB por cada bit.

La salida del cuantificador se envía a un codificador, que asigna un número binario único (palabra de código) a cada nivel de cuantización. Se puede utilizar cualquier asignación de palabras de código a niveles y existen muchos esquemas de codificación. Mayoría Los sistemas de procesamiento de señales digitales utilizan la representación en complemento a dos. En este sistema, con un bit (B + 1) palabra clave,

c = [bo,hl,. .. , bB]

el bit más a la izquierda o más significativo, bo, es el bit de signo, y los bits restantes se utilizan para representar binarios enteros o fracciones. Suponiendo fracciones binarias, la palabra clave boblb2 .. . bs tiene el valor 

A continuación se proporciona un ejemplo para una palabra de código de 3 bits.

I Símbolo binario Valor numérico I 

3.3 Conversión de digital a analógico 

 Como se establece en el teorema de muestreo, si x,(t) está estrictamente limitada en banda, de modo que Xa(jSZ) = 0 para Is21 > no, y si T, < T/QO, entonces xa(t) puede reconstruirse de forma única a partir de sus muestras x(n) = x,(nT,). El proceso de reconstrucción consta de dos pasos, como se ilustra en la figura 3-6. Primero, las muestras x(n) se convierten en una secuencia de impulsos,

y luego x,(t) se filtra con un filtro de reconstrucción, que es un filtro de paso bajo ideal que tiene una respuesta de frecuencia dada por 

Este sistema se denomina convertidor ideal discreto a continuo (DIC). Debido a que la respuesta al impulso de la el filtro de reconstrucción es 

 

Figura 3-6. (a) Un convertidor discreto a continuo con un filtro de reconstrucción de paso bajo ideal. (h) El respuesta de frecuencia del filtro de reconstrucción ideal.

la salida del filtro es 

Esta fórmula de interpolación muestra cómo se reconstruye x,(t) a partir de sus muestras x(n) = x,(nTs). en la frecuencia dominio, la fórmula de interpolación se convierte en

que es equivalente a 

Por lo tanto, x (eiw) se escala en frecuencia (o = QTS), y luego el filtro de paso bajo elimina todas las frecuencias en el periódico espectro x(eiQTr) por encima de la frecuencia de corte Q,. = TETAS,.

Debido a que no es posible implementar un filtro de paso bajo ideal, muchos convertidores D/A utilizan una retención de orden cero. para el filtro de reconstrucción. La respuesta al impulso de una retención de orden cero es 

y la respuesta de frecuencia es 

Después de convertir una secuencia de muestras xa(nT,) en impulsos, la retención de orden cero produce la escalera aproximación a xu(!) que se muestra en la figura 3-7. Con una retención de orden cero, es común posprocesar la salida con un filtro de compensación de reconstrucción que se aproxima a la respuesta de frecuencia 

Figura 3-7. El uso de una retención de orden cero para interpolar entre las muestras en x,(t).

de modo que la cascada de Ho(ejo) con HC(ejw) se aproxima a un filtro paso bajo con una ganancia de T, sobre la banda de paso. La figura 3-8 muestra la magnitud de la respuesta de frecuencia de la retención de orden cero y la magnitud de la respuesta de frecuencia del filtro de compensación de reconstrucción ideal. Nótese que la cascada de H,(jn) con el la retención de orden cero es un filtro de paso bajo ideal. 

/Filtro de interpolación ideal

Retención de orden cero 

Figura 3-8. (a) La magnitud de la respuesta de frecuencia de un orden cero mantener en comparación con el filtro de reconstrucción ideal. (b) El filtro de compensación de reconstrucción ideal.

3.4 Procesamiento en tiempo discreto de señales analógicas 

 Una de las aplicaciones importantes de los convertidores AD y D/A es el procesamiento de señales analógicas con un sistema de tiempo discreto. En el caso ideal, el sistema completo, que se muestra en la figura 3-9, consiste en la cascada de un convertidor C/D, un sistema de tiempo discreto y un convertidor D/C. Por lo tanto, asumimos que la señal muestreada no está cuantificada y que se utiliza un filtro de paso bajo ideal para el filtro de reconstrucción en el convertidor D/C. porque la entradaxa(t) y la salida ya(t) son señales analógicas, el sistema total corresponde a un sistema de tiempo continuo. A

analice este sistema, observe que el convertidor C/D produce la señal de tiempo discreto x(n), que tiene una DTFT dada por

Si el sistema de tiempo discreto es lineal e invariante al cambio con una respuesta de frecuencia H(ejW), 

Figura 3-9. Procesamiento de una señal analógica utilizando un sistema de tiempo discreto.

Finalmente, el convertidor D/C produce la señal de tiempo continuo y,(t) a partir de las muestras y(n) de la siguiente manera: 

Ya sea usando la Ec. (3.7) o tomando la DTFT directamente, en el dominio de la frecuencia esta relación se convierte en 

o 

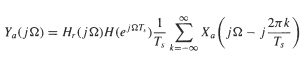
Si x,(t) está limitado en banda con X,(jQ) = 0 para IQI > TIT,, el filtro de paso bajo H,(jQ) elimina todos los términos en el suma excepto la primera, y 

Por lo tanto, el sistema total se comporta como un sistema de tiempo continuo lineal e invariante en el tiempo con una respuesta de frecuencia efectiva 

Así como un sistema de tiempo continuo puede implementarse en términos de un sistema de tiempo discreto, también es posible implementar un sistema de tiempo discreto en términos de un sistema de tiempo continuo como se ilustra en la figura 3-10. La señal x,(t) está relacionado con los valores de secuencia x(n) de la siguiente manera: 

Figura 3-10. Procesamiento de una señal en tiempo discreto usando un sistema en tiempo continuo.

Debido a que x,(t) tiene un límite de banda, y,(t) también tiene un límite de banda y puede representarse en términos de sus muestras de la siguiente manera: 

La relación entre la transformada de Fourier de xa(t) y la DTFT de x(n) es 

y la relación entre las transformadas de Fourier de x, (t) y ya(t) es

Por lo tanto, 

y la respuesta de frecuencia del sistema de tiempo discreto equivalente es 

3.5 Conversión de frecuencia de muestreo 

 En muchas aplicaciones prácticas del procesamiento de señales digitales, uno se enfrenta al problema de cambiar el muestreo. tasa de una señal. El proceso de convertir una señal de una frecuencia a otra se denomina conversión de frecuencia de muestreo.Hay dos formas de realizar la conversión de frecuencia de muestreo. Primero, la señal muestreada se puede volver a convertir en una señal analógica y luego se vuelve a muestrear. Alternativamente, la señal se puede volver a muestrear en el dominio digital. Este enfoque tiene la ventaja de no introducir distorsión adicional al pasar la señal a través de un adicional Conversor D/A y AD. En esta sección, describimos cómo se puede realizar digitalmente la conversión de frecuencia de muestreo.

3.5.1 Reducción de la frecuencia de muestreo por un factor entero 

 Supongamos que nos gustaría reducir la tasa de muestreo por un factor entero, M. Con un nuevo período de muestreo T,' = MT,, la señal remuestreada es 

Por lo tanto, la reducción de la tasa de muestreo por un factor entero M se puede lograr tomando cada M-ésima muestra de x(n). El sistema para realizar esta operación, llamado down-sampler, se muestra en la figura 3-1 l(a). Down-sampling generalmente resulta en aliasing. Específicamente, recuerda que la DTFT de x(n)= x,(nT,) es

Del mismo modo, el DTFT de x &) = x (nM) = x, (n M T,) es 

Tenga en cuenta que el índice de suma r en la expresión de Xd(ejo) puede expresarse como

r=i+kM 

Figura 3-11. (a) Muestreo descendente por un factor entero M. (b) Diezmación por un factor de M, donde H(ejU) es un filtro de paso bajo con una frecuencia de corte 

donde -oo < k < oo y 0 5 i 5 M - 1. Por lo tanto, Xd(eJW) puede expresarse como

El término dentro de los corchetes es 

Así, la relación entre x(ejw) y Xd (ejw) es

Por lo tanto, para evitar el aliasing, x(n) debe filtrarse antes del muestreo descendente con un filtro de paso bajo. que tiene una frecuencia de corte o,.= n/M. La cascada de un filtro de paso bajo con un muestreador descendente ilustrado en La figura 3-11(b) se llama diezmador.

3.5.2 Aumento de la frecuencia de muestreo por un factor entero 

 Supongamos que nos gustaría aumentar la tasa de muestreo por un factor entero L. Si xa(t) se muestrea con un frecuencia de muestreo fs = I / T,, entonces x(n) = xa(nTs)

Para aumentar la frecuencia de muestreo en un factor entero L, es necesario extraer las muestras 

de x(n). Las muestras de x;(n) para valores de n que son múltiplos enteros de L se extraen fácilmente de x(n) como sigue: 

En la figura 3-12(a) se muestra un muestreador ascendente que produce la secuencia 

En otras palabras, el muestreador ascendente expande la escala de tiempo por un factor de L insertando L - 1 ceros entre cada muestra de x(n). En el dominio de la frecuencia, el muestreador ascendente se describe mediante 

Por lo tanto, X(eJW) simplemente se escala en frecuencia. Después del muestreo ascendente, es necesario eliminar la frecuencia imágenes escaladas de X,(jQ), excepto aquellas que son múltiplos enteros de 2x. Esto se logra filtrando Z;(n)

Fig. 3-12. (a)Up-sampling by an integer factor L. (b)Interpolation by a factor of L

con un filtro de paso bajo que tiene una frecuencia de corte de n/L y una ganancia de L. En el dominio del tiempo, el filtro de paso bajo interpola entre las muestras en múltiplos enteros de L como se muestra en la figura 3-13. La cascada de un up-sampler con un filtro de paso bajo que se muestra en la figura 3-12(b) se llama interpolador. El proceso de interpolación en la frecuencia. el dominio se ilustra en la figura 3-14 

Figura 3-13. (a) La salida del muestreador ascendente. (b) La interpolación entre las muestras T,(n)que se realiza mediante el filtro de paso bajo

Figura 3-14. Ilustración en el dominio de la frecuencia del proceso de interpolación. (a) El señal de tiempo continuo. (b) La DTFT de la señal muestreada x(n) = x,(nT,). (c) La DTFT de la salida del muestreador ascendente. (d) El filtro de paso bajo ideal para realizar la interpolación. (e) La DTFT de la señal interpolada. 

3.5.3 Conversión de frecuencia de muestreo por un factor racional 

La cascada de un diezmador que reduce la tasa de muestreo por un factor de M con un interpolador que aumenta la tasa de muestreo por factor vital de L da como resultado un sistema que cambia la tasa de muestreo por un factor racional de L/M. Esta cascada se ilustra en la figura 3-15(a). Porque la cascada de dos filtros de paso bajo con corte frecuencias n/M y n/Lis equivalentes a un solo filtro de paso bajo con una frecuencia de corte

el convertidor de frecuencia de muestreo se puede simplificar como se ilustra en la figura 3-15(b). 

Figura 3-15. (a) Cascada de un interpolador y un diezmador para cambiar la tasa de muestreo por un factor racional LIM.

(b) Una estructura simplificada que resulta cuando se combinan los dos tiltros de paso bajo.

EJEMPLO 3.5.1 Suponga que se ha muestreado una señal x,,(t) con una frecuencia de muestreo de 8 kHz y que quisiera derivar la señal de tiempo discreto que se habría obtenido si xu(!) se hubiera muestreado con una frecuencia de muestreo de 10kHz Por lo tanto, nos gustaría cambiar la tasa de muestreo por un factor de 

Esto puede lograrse aumentando el muestreo de x(n) por un factor de 5, inclinando la señal muestreada con un filtro de paso bajo que tiene una frecuencia de corte w, = n/5 y una ganancia de 5, y luego reduce el muestreo de la señal filtrada por un factor de 4.

Problemas Resueltos 

 Conversión AID y DIA

3.1 Considere la secuencia de tiempo discreto

Encuentre dos señales de tiempo continuo diferentes que producirían esta secuencia cuando se muestrean a una frecuencia

apagado, = 10 Hz.

Una sinusoide de tiempo continuo

.%(I) =COS(QOI)= cos(2nfat)

que se muestrea con una frecuencia de muestreo desactivada, da como resultado la secuencia de tiempo discreto

Sin embargo, observe que para cualquier entero k,

cos (2rr -n = cos (2n -fofkf'n)

fs

Por lo tanto, cualquier sinusoide con una frecuencia

CAP. 31 MUESTREO 115

producirá la misma secuencia cuando se muestree con una frecuencia de muestreo f,. Con x(n) = cos(nn/8), queremos

o fo = i!g fs = 625 Hz

Por lo tanto, dos señales que producen la secuencia dada son

x,(t) = cos(1250nf)

y .r2(t)=cos(21250nt)

3.2 Si la tasa de Nyquist para xa(t) es a, ¿cuál es la tasa de Nyquist para cada una de las siguientes señales que son

derivado de xa(r)?

dxa(t) (a) 7

(b) xa (2t)

(c) ~,2(t)

(4 xa0) cos(Qot)

(a) La tasa de Nyquist es igual al doble de la frecuencia más alta en x,(t). Si

entonces Y,(jSt) = jStX,(jQ)

Así, si X,(jR) = 0 para IQI > Sto, lo mismo será cierto para Y,(jR). Por lo tanto, la frecuencia de Nyquist no es

cambiado por la diferenciación.

(b) La señal ya(t) = xa(2t) se forma a partir de x,(t) comprimiendo el eje del tiempo por un factor de 2. Esto da como resultado una

expansión del eje de frecuencia por un factor de 2. Específicamente, tenga en cuenta que

En consecuencia, si la frecuencia de Nyquist para x,(r) es St,, la frecuencia de Nyquist para y&) será 2S2,.

(c) Cuando se multiplican dos señales, sus transformadas de Fourier se convolucionan. Por lo tanto, si

Así, la frecuencia más alta en yo([) será el doble de la de x,,(r), y la frecuencia de Nyquist será 2Q,.

(d) La modulación de una señal por cos(Qol) desplaza el espectro de xa(l) hacia arriba y hacia abajo en no. Por lo tanto, el Nyquist

frecuencia para ya(t) = cos(Qot)xa(r)será S2, + 2Qo.

116 MUESTREO [CAP. 3

3.3 Sea h,(t) la respuesta al impulso de un filtro causal de tiempo continuo con una función de sistema

Así, H,(s) tiene un cero en s = -a y un par de polos en s = -a kjh. Muestreando h,(t) formamos un

filtro de tiempo discreto con una respuesta de muestra unitaria

Encuentre la respuesta de frecuencia H(ejw) del filtro de tiempo discreto.

Para encontrar la respuesta de frecuencia H(eJU),es necesario encontrar la respuesta de impulso del filtro analógico, h,(t),muestra

la respuesta al impulso,

h(n)= h,(nT,)

y luego encontrar la transformada de Fourier en tiempo discreto,

Para encontrar la respuesta al impulso, primero realizamos una expansión en fracciones parciales de Ha(s) de la siguiente manera:

un b

Ha(s)= s +(a + jb) + s +(a -jb)

La constante A es

De manera similar, para B tenemos

-

yo yo

Por tanto, Ha(s)= s +(a + jb) + s + (a2- jb)

Otra forma de encontrar las constantes A y B sería escribir la Ec. (3.13) sobre un denominador común,

s+a = A(s +a -jb) + B(s +a + jb) Ha(s)= (s + + b2 (s +a)2+ b2

e igualar los coeficientes polinómicos en los numeradores de H,(s):

A+B=yo

A(a -jb) + B(a + jb) = a

Resolver estas dos ecuaciones para A y B da el mismo resultado que antes. A partir de la expansión en fracciones parciales de

Ha(s), la respuesta al impulso se puede encontrar usando el par de transformadas de Laplace

CAP. 31 MUESTREO

Muestreando ha(! ), tenemos

h(n) = h,(nT,) = e-a"T~os(bn~s)u(n)

Finalmente, para la respuesta de frecuencia tenemos

Tenga en cuenta que para que estas sumas converjan y para que exista la respuesta de frecuencia, es necesario que

le-aTs( < yo

o, debido a que T, > 0, debemos tener a > 0. En otras palabras, los polos de H,(s) deben estar en la mitad izquierda del plano s o,

equivalentemente, h,,(t) debe ser un filtro estable. Con a > 0 tenemos

que, después de combinar sobre un denominador común y simplificar, da

3.4 Un filtro de tiempo continuo tiene una función de sistema

Si h,(t) se muestrea para formar un sistema de tiempo discreto con una respuesta de muestra unitaria

h(n) = ha(nT7)

encuentre el valor de Ts de modo que ~(e.~") en w = rr/2 esté 6 dB por debajo de su valor máximo en w = 0, es decir,

IH (eJT'2)12 10 log = -6 IH (eio)12

La respuesta al impulso del sistema de tiempo continuo es

h,(t) = e-'u(t)

Cuando se muestrea con un período de muestreo T,, la respuesta de la muestra unitaria resultante es

h(n) = h,,(nT,) = e-"%u(n)

y la respuesta de frecuencia es

MUESTREO [CAP. 3

Con

y

se deduce que queremos

~H(e~~f~)l~ -c-&)~= -6 lo log I H(ej0)12 = lolog (1

1 + ecZT

Así, tenemos

1 - 2KTs + e-2T' = 0,2512 [I + e-2T']

o 0.7488e-~~'- 2KT' + 0.7488 = 0

que es una ecuación cuadrática en ed. Resolviendo para las raíces de esta ecuación cuadrática, encontramos

Tomando el logaritmo natural y seleccionando el valor positivo de T, tenemos

T, = 0,7978

3.5 Una señal de tiempo continuo xa(t) tiene una banda limitada con X,(jS1) = 0 para IS11 > no. Si xa(t) se muestrea con

una frecuencia de muestreo S1, 2 2Slo, ¿cómo es la energía en x(n),

relacionado con la energía en xa(t), W

y el período de muestreo T,?

Usando el teorema de Parseval, la energía en la señal analógica x,(t) puede expresarse en el dominio de la frecuencia de la siguiente manera:

Como x,(t) tiene una banda limitada con X,(jQ) = 0 para Is21 Go,

El muestreo de x,(t) a la tasa de Nyquist o superior da como resultado una secuencia x(n) con una transformada de Fourier de tiempo discreto

CAP. 31 MUESTREO

Por lo tanto, la energía en x(n), usando el teorema de Parseval, es

y tenemos

I

E,, = -E,

ts

Como verificación de este resultado. supongamos que x,(t) es a by señal limitada con un espectro que se muestra en la siguiente figura.

t """"'

La energía en x, (I) es

Cuando se muestrea con una frecuencia de muestreo Q, 1 2Qo, la DTFT de la señal muestreada es como se muestra en la siguiente

cifra:

Por lo tanto, la energía en x(n) es

3.6 Una señal analógica de paso de banda compleja xa(t) tiene una transformada de Fourier distinta de cero en el rango de frecuencia

[Ql,Q2] como se muestra en la siguiente figura.

La señal se muestrea para producir la secuencia x(n) = xa(nT,).

(a) ¿Cuál es la frecuencia de muestreo más pequeña que puede usarse para que xa(t) pueda recuperarse de su

muestras x(n)?

MUESTREO [CAP. 3

(b) Para esta frecuencia mínima de muestreo, encuentre la fórmula de interpolación para x,(t) en términos de x(n).

(a) Como la frecuencia más alta en xa(t) es Q2, la tasa de Nyquist es 2Q2. Sin embargo, tenga en cuenta que si xa(t) se modula

con una exponencial compleja de frecuencia (Q2 + Q1)/2,

entonces y,(t) es una señal de paso bajo (compleja) con un espectro que se muestra en la siguiente figura:

A Yu(jQ)

donde Qo = (Q2 - Q1)/2. Por lo tanto, la tasa de Nyquist para yo(() es 2Q0 = Q2 -Ql, lo que sugiere que x,(t) puede

ser reconstruido de forma única a partir de sus muestras x,(nT,) siempre que

Si xa(t) se muestrea con una frecuencia de muestreo Q,, el espectro de la señal muestreada es

como se ilustra a continuación.

QI -% Q2-Qs QI Q2

Para que no haya interferencia entre los espectros desplazados, es necesario que

Si se cumple esta condición, xa(t) puede reconstruirse de forma única a partir de xs(t) usando un filtro de paso de banda con un

respuesta de frecuencia como se muestra a continuación.

(b) Con una frecuencia de muestreo Q, = Q2-Ql, el filtro de reconstrucción es un filtro de paso de banda complejo con un impulso

respuesta

ha(!) = Ts sin(Qst/2)e-j(~2+~~~ Trt

CAP. 31 MUESTREO

Por lo tanto, la salida del filtro de reconstrucción, que produce la señal de paso de banda compleja x,(t), es

3.7 Dada una señal de paso de banda de valor real x,(t) con Xa(f) = 0 para If l < fi y If 1 > f2, el Nyquist

El teorema de muestreo dice que la frecuencia mínima de muestreo es fs = 2 f2. Sin embargo, en algunos casos, el

la señal se puede muestrear a una velocidad más baja.

(a) Suponga que fl = 8 kHz y f2 = 10 kHz. Haz un bosquejo de la transformada de Fourier en tiempo discreto

de x(n) = x,(nTs) si fs = I /T, = 4 kHz.

(6) Defina el ancho de banda de la señal pasabanda a ser

y la frecuencia central a ser

Muestre que si f, > B/2 y f2 es un múltiplo entero del ancho de banda B, no ocurrirá aliasing si

xa(t) se muestrea a una frecuencia de muestreo fs = 28.

(c) Repita el inciso (b) para el caso en que f2 no sea un múltiplo entero del ancho de banda B.

(a) Sea xu([) un espectro como el que se muestra en la siguiente figura.

El espectro de la señal muestreada

que se forma desplazando X,(f) por múltiplos enteros de la frecuencia de muestreo y sumando. Con f, =

4 kHz, tenemos el espectro esbozado a continuación.

kHz

Tenga en cuenta que X,( f) no tiene alias. Por lo tanto, con el procesamiento apropiado de x,(r), la señal x,(r) puede ser

recuperado de sus muestras. Finalmente, la DTFT de la secuencia de tiempo discreto x(n) = x,(nTs) es

MUESTREO [CAP. 3

que se esboza a continuación.

,x(c'")

(b) Si fi es un múltiplo entero de B, podemos expresar fi y f2 como sigue:

Con una frecuencia de muestreo de f,= 2B, la señal muestreada tiene un espectro

Como Xa(f) es distinto de cero solo para (I -l)B < Si 1 < lB, solo hay un término en la suma que contribuye a

X,( f) en el rango de frecuencia O< f <B y solo un término que contribuye al rango de frecuencia -B si < 0

(haga un dibujo como en la parte (a) para verlo claramente). Por lo tanto, no hay aliasing, y x,(t) puede ser muestreado

sin aliasing si una frecuencia de muestreo f, = 2B.

(c) Si f2 no es un múltiplo entero de B, siempre podemos aumentar B hasta que este sea el caso. Específicamente, deja

donde 1.1 se define como la "parte entera". Ahora, si simplemente incrementamos B a B' donde

tenemos el caso descrito en la parte (b) donde fi es un múltiplo entero del ancho de banda. Así, x,(t) puede ser

muestreado sin aliasing una frecuencia de muestreo de

3.8 Determine la frecuencia de muestreo mínima para cada una de las siguientes señales de paso de banda:

(a) xa(t) es real con Xu(f) distinto de cero solo para 9 kHz < (f1 < 12 kHz.

(b) xa(t) es real con Xu(f) distinto de cero sólo para 18 kHz < 1 f 1 < 22 kHz.

(c) xa(t) es complejo con X,(f) distinto de cero solo para 30 kHz < f < 35 kHz.

(a) Para esta señal, el ancho de banda es B = f2 -fl = 3 kHz, y f2 = 12 = 4B es un múltiplo entero de B.

Por lo tanto, la frecuencia mínima de muestreo es f, = 2B = 6 kHz.

(b) Para esta señal, B = 4 kHz y f2 = 22, que no es un múltiplo entero de B. Con Lfi/B1 = 5, si hacemos

B' = f2/5 = 4.4, f2 es un múltiplo entero de B', y .ra(t) puede muestrearse con una frecuencia de muestreo de

f, = 28' = 8,8 kHz.

(c) Para una señal de paso de banda compleja con un espectro distinto de cero para fi < f < f2, el muestreo mínimo

la frecuencia es f, = f2 -fl. Así, para esta señal, f,= 5 kHz.

3.9 ¿Cuántos bits se necesitan en un convertidor A/D si queremos una relación señal/ruido de cuantificación de al menos

90dB? Suponga que xa(t) es gaussiana con una varianza a:, y que el rango del cuantificador se extiende desde

-3a, a 3ax; es decir, X,,, = 30; (con este valor para X,,,, solo alrededor de uno ode cada 1000 muestras

excederá el rango del cuantificador).

CAP. 31 MUESTREO

Para un cuantificador de bits (B + I), la relación señal-ruido de cuantificación es

x m,, SQNR = 6,02B + 10,81 - 2010g -

4r

Con X,,, = 30, esto se convierte en

SQNR = 6,02B + 10,81 - 20l0g3 = 6,02B + 10,81 -9,54 = 6,02B + 1,27

Si queremos una relación señal-ruido de cuantificación de 90 dB, requerimos

3.10 Se debe muestrear una imagen con una relación señal/ruido de cuantificación de al menos 80 dB. A diferencia de muchos otros

señales, las muestras de imagen no son negativas. Suponga que el dispositivo de muestreo está calibrado de modo que la

las intensidades de la imagen muestreada caen dentro del rango de 0 a 1. ¿Cuántos bits se necesitan para lograr el

relación señal-ruido de cuantificación deseada?

Para una señal bipolar con amplitudes que caen dentro del rango [-X,,,,, X,,,], la relación señal-ruido de cuantificación

es

SQNR = 6.02B + 10.81 - 201og&

0,

Para una señal no negativa que está confinada al intervalo [0, I], la relación señal-ruido de cuantificación es equivalente a

el caso bipolar si hacemos X,,, = 0.5. Si suponemos que las intensidades de la imagen se distribuyen uniformemente sobre

el intervalo [0, I],

u2 = yo r 12

rn Por lo tanto, SQNR = 6.02B + 10.81 -2010g -= 6.02B + 6.03 2

y para una relación señal-ruido de cuantificación de 80 dB, requerimos

o B + 1 = 14 bits.

3.11 Suponga que tenemos un conjunto de muestras no cuantificadas, x(n), que son no negativas para todo n. Un método para

la cuantificación de x(n) que se usa a menudo en el procesamiento del habla es la siguiente. Primero formamos la secuencia

y(n) = log[x(n)l

Entonces y(n) se cuantifica con un cuantificador uniforme de (B + 1) bits,

9(n) = C?[y(n)l = y(n) + e(n)

Las muestras de señal cuantificadas se obtienen luego exponenciando J(n),

W) = exp(9(n))

Demuestre que si 'e(n) es pequeño, la relación señal/ruido de cuantificación es independiente de la potencia de la señal.

MUESTREO

tenemos, para R(n),

R(n) = exp{log[x(n)l +e(n)} = x(n) .exp(e(n))

Si e(n) << 1, podemos usar la expansión

exp{e(n)) x 1 + e(n)

escribir

&n) = x(n)l I+e(n)] = x(n) + f (n)

donde f (n) = x (n) e (n) es un ruido de cuantificación (dependiente de la señal). Si asumimos que el ruido de cuantificación e(n) es

estadísticamente independiente de x(n),

Elf2(n)) = ~{x~(n)}. E{e2(n))

y la relación señal-ruido de cuantificación es

E{x2(n)l SQNR = 10 log -= -10 log E (e2(n)) E{f '(n))

que es independiente de la potencia de la señal.

Procesamiento en tiempo discreto de señales analógicas

Se va a filtrar una señal de tiempo continuo xa(t) para eliminar los componentes de frecuencia en el rango de 5 kHz5 f i

10kHz La frecuencia máxima presente en xa(t) es de 20 kHz. El filtrado se hará por muestreo.

x,(t), filtrando la señal muestreada y reconstruyendo una señal analógica utilizando un convertidor D/C ideal. Encontrar

la frecuencia de muestreo mínima que se puede utilizar para evitar el aliasing, y para este muestreo mínimo

tasa, encuentre la respuesta de frecuencia del filtro digital ideal H(eJm) que eliminará las frecuencias deseadas

de xa(t).

Debido a que la frecuencia más alta en x,(t) es de 20 kHz, la frecuencia de muestreo mínima para evitar el solapamiento es f, = 40 kHz.

La relación entre la variable de frecuencia continua R y la variable de frecuencia discreta o viene dada por

Por lo tanto, el rango de frecuencia 5 kHz 5 f 5 10 kHz corresponde a un rango de frecuencia digital

y el filtro digital deseado es un filtro de supresión de banda que tiene una respuesta de frecuencia como se ilustra en la figura siguiente.

3.13 Un problema importante en el registro de electrocardiogramas (ECG) es la aparición de

Interferencia de 60 Hz en la salida. Las causas de esta interferencia de la línea eléctrica incluyen la inducción magnética, las corrientes de desplazamiento en los cables del cuerpo del paciente y las interconexiones del equipo.

Suponga que el ancho de banda de la señal de interés es de 1 kHz, es decir,

CAP. 31 MUESTREO 125

La señal analógica se convierte en una señal de tiempo discreto con un convertidor A/D ideal que funciona con

una frecuencia de muestreo tY. La señal resultante x(n) = x,(nTs) se procesa luego con un tiempo discreto

sistema que se describe mediante la ecuación en diferencias

La señal filtrada, y(n), luego se vuelve a convertir en una señal analógica utilizando un convertidor D/A ideal. Diseño

un sistema para eliminar la interferencia de 60 Hz especificando valores para f, a y b para que una señal de 60 Hz

de la forma

w,(t) = A sin(l20nt)

no aparecerá en la salida del convertidor D/A.

La señal a la que se eliminará el ruido de 60 Hz tiene una banda limitada a 1000 Hz. Por lo tanto, para evitar el aliasing

cuando se muestrea la señal, necesitamos una frecuencia de muestreo

Usando la tasa mínima de 2000 Hz, observe que una señal de 60 Hz wo(t) = sin(l20nt) se convierte en

donde = 0.06n. Recuerde que las exponenciales complejas son funciones propias de sistemas lineales invariantes por desplazamiento. Por lo tanto,

si la entrada a un sistema LSI es x(n) = eJn"O, la salida es

Porque

w(n) se eliminará de x(n) si diseñamos un filtro para que H(ejw) sea igual a cero en w = fwo. Porque H(eJw) es

un filtro de segundo orden con una respuesta de frecuencia

se puede factorizar de la siguiente manera:

H(eJ") = (1 -~e-~")(l-fie-]")

Por lo tanto, H (ejw) será cero para w = fwo si a! = eJw y B = e--1". En este caso, tenemos

el nosotros, nuestros requisitos son que

a = -2 cos wo = -2 cos(0.06n) h = 1

y f, = 2000.

3.14 El siguiente sistema se utiliza para procesar una señal analógica con un sistema de tiempo discreto.

yo yo

xo(r) Tiempo discreto YO@)

CP Sistema 'y) D/C -

MUESTREO [CAP. 3

Suponga que xa(t) tiene una banda limitada con X,( f) =0 para Si 1 > 5 kHz como se muestra en la figura a continuación,

+ Xdf)

y que el sistema de tiempo discreto es un filtro de paso bajo ideal con una frecuencia de corte de n/2.

Encuentre la transformada de Fourier de ya(t) si las frecuencias de muestreo son fl = f2 = 10 kHz.

Repita para fl = 20 kHz y f2 = 10 kHz.

Repita para fl = 10 kHz y f2 = 20 kHz.

Cuando las frecuencias de muestreo de los convertidores C/D y D/C son las mismas, y x,(t) tiene una banda limitada con

X,(jS2) =0 para If21 > n/Tl, este sistema es equivalente a un filtro analógico con respuesta en frecuencia

Por lo tanto, si ~(ej") es un filtro de paso bajo con una frecuencia de corte de 71/2, la frecuencia de corte de Ha(jf2), denotada

por no, está dado por

Por lo tanto, fo = fl = 2500 Hz

Cuando las frecuencias de muestreo de C/D y D/C son diferentes, es mejor trazar el espectro de las señales como

progresan a través del sistema. Wilh X,( f) como se muestra arriba, la transformada de Fourier en tiempo discreto de x(n) es

Debido a que la frecuencia de corte del filtro de paso bajo de tiempo discreto es n/2, y(n) =x(n), y la salida del D/C

convertidor es como se muestra a continuación.

Con fi = 10 kHz, estamos muestreando xu([) a la tasa de Nyquist, y el espectro de x(n) es

+ XkJ")

CAP. 31 MUESTREO

y la salida del filtro de paso bajo es como se muestra a continuación.

+ y(el")

Por lo tanto, el espectro de yo(() es el siguiente:

+ Ya(f)

3.15 Considere el sistema de la figura 3-9 para implementar un sistema de tiempo continuo en términos de un sistema de tiempo discreto

sistema. Suponga que la entrada al convertidor C/D está limitada en banda a Q0 = Q,/2 y que la muestra unitaria

La respuesta del sistema de tiempo discreto es

Encuentre la respuesta de frecuencia general de este sistema.

Suponiendo entradas de banda limitada con X,(JR) = 0 para (R(> Rs/2, la salida Ya(jR) está relacionada con la entrada X,(jS2)

como sigue:

ya(jQ) = HJjR)X(JQ)

Debido a que la respuesta de frecuencia del sistema de tiempo discreto es

H(el")= I - 0.9e-I"

ÉL

entonces H"(;n) =

de lo contrario

3.16 Considere el sistema que se muestra en la figura 3-9 para implementar un sistema de tiempo continuo en términos de un sistema de tiempo discreto. Suponiendo que las señales de entrada x,(t) tienen una banda limitada, de modo que X,( f) = 0 para (f( > 10 kHz,

encontrar el sistema de tiempo discreto que produce la salida

Iflx,(f> 20005Ifli8000

r,(f) = de lo contrario

Para entradas de banda limitada, el sistema de la figura 3-9 es un sistema lineal invariante por desplazamiento con una respuesta de frecuencia efectiva

igual a

El sistema que nos gustaría realizar tiene una respuesta de frecuencia

(:I 40001~1 In1 5 I sooh

Ha(jQ)= en caso contrario

MUESTREO [CAP. 3

Si asumimos una frecuencia de muestreo f, = 20 kHz, la respuesta de frecuencia del sistema de tiempo discreto debe ser

W 0,2~5 101 50,8~

de lo contrario

donde T, = 1/20000.

3.17 En la siguiente figura se muestra un diagrama de una red híbrida digital-analógica.

El sistema de tiempo discreto H(eJW) es un filtro de paso bajo

A I 4 5 o o ~(e")= {0 más

y el sistema analógico Hhpf(f) es un filtro de paso alto con una respuesta de frecuencia como la que se muestra a continuación.

t "'"'

La entrada xa(r) tiene un límite de banda de 4 kHz y las frecuencias de muestreo de los convertidores CP y DIC ideales

son 10 kHz. Encuentre el valor para A y q que resultará en una reconstrucción perfecta de xa(t),

Debido a que xa(t) tiene un límite de banda de 4 kHz, la rama superior de este sistema híbrido actúa como un filtro de paso bajo analógico ideal.

con una respuesta de frecuencia

Debido a que la red analógica es un filtro de paso alto con una frecuencia de corte de 4 kHz y

&(t) será igual a xa(t) siempre que A = 1 y

3.18 Se va a transmitir una secuencia digital x(n) a través de un canal de banda limitada lineal e invariable en el tiempo, como se ilustra

en la figura de abajo.

CAP. 31 MUESTREO

Transmisor Receptor

El transmisor es un convertidor D/C y el receptor simplemente muestrea la forma de onda recibida y,(r):

Suponga que el canal se puede modelar como un filtro de paso bajo ideal con una frecuencia de corte de 4 kHz:

(a) Suponiendo un C P y D/C ideales, y una sincronización perfecta entre el transmisor y el receptor,

¿Qué valores de T, (si los hay) garantizarán que y(n) = x(n)?

(b) Suponga que D/C no es ideal. Específicamente, suponga que x(n) se convierte primero en un impulso

entrenar y luego se usa una retención de orden cero para realizar la "interpolación" entre los valores de muestra.

En otras palabras, la respuesta de impulso del filtro de interpolación es un pulso de duración T,:

1 051iT'

Mt) = 0 en caso contrario

Debido a que la secuencia recibida y(n) ya no será igual a x(n), para mejorar el rendimiento del receptor, las muestras recibidas se procesan con un filtro digital como se muestra a continuación.

Encuentre la respuesta de frecuencia del filtro que debe usarse para filtrar y(n).

(a) La salida del convertidor D/C es una señal de banda limitada xa(t) con una transformada de Fourier que es igual a cero para

Si 1 > fs/2. Debido a que xa(t) pasa a través de un canal de banda limitada que rechaza todas las frecuencias mayores que

4 kHz, para que no haya distorsión en el receptor, es necesario que

De este modo , los convertidores C/D y D/C deben funcionar a una velocidad inferior a 8 kHz.

(b) Para obtener la máxima cantidad de datos a través del canal por unidad de tiempo, dejaremos que T sea el mínimo

periodo de muestreo,

Ts = &,

Cuando el filtro de reconstrucción en el convertidor D/C es de orden cero, la respuesta de frecuencia del sistema de tiempo discreto que relaciona la secuencia de entrada x(n) con la secuencia reconstruida y(n) es

MUESTREO [CAP. 3

dónde

yo 0 de lo contrario

Por lo tanto,

y el filtro de tiempo discreto para procesar y(n) para eliminar la distorsión introducida por la retención de orden cero debería

aproximar la respuesta

3.19 Considere el siguiente sistema para procesar una señal de tiempo continuo con un sistema de tiempo discreto:

La respuesta de frecuencia del filtro de tiempo discreto es

Iff, = 2 kHz y x,(t) = sen(1000~t), encuentre la salida y,(t).

Muestrear n,(r) = sen(10007rr) con una frecuencia de muestreo f, = 2000 produce la secuencia de tiempo discreto

x(n) =x,(nT,) = sen(10007rnTs) = sen -

(3

Esta secuencia luego se filtra con el filtro de tiempo discreto

Como x(n) es una sinusoide, la respuesta es

donde A y 4 son la magnitud y la fase, respectivamente, de la respuesta de frecuencia en o = 1712. Con

$-;coso = 4

(I - e ) (I -I ) - COSO

se sigue que I H (ejw)l = 2. Podemos evaluar la fase de la siguiente manera:

CAP. 3) MUESTREO

8 sln w Por lo tanto. 4,,(~)= tan-' ;-$ cos,

que, cuando se evalúa en o = n/2, da

4,, (w)J,=,/~ = tan-' = tan-' = 0,2952~

Así, y(n) = 2sen(:[n +0.59031)

3.20 Considere el siguiente sistema que consta de un convertidor D/C ideal, un filtro lineal invariante en el tiempo y un

convertidor CP ideal.

El sistema de tiempo continuo h,(t) es un filtro de paso bajo ideal con una respuesta de frecuencia

1 If1 5 1OkH.z

Hdf) = yo de lo contrario

(a) Si TI = T2 = encuentre una expresión que relacione la salida y(n) con la entrada x(n).

(b) Si TI = (a) x y T2 = encuentre y(n) cuando

(a) Cuando TI = T2, este sistema se comporta como un sistema de tiempo discreto invariante con desplazamiento lineal con una respuesta de frecuencia

Porque H,(jS2) = 1 para 152) < 2n. lo4,

y h(n) = 6(n)

Por lo tanto, y(n) =x(n).

Otra forma de analizar este sistema es notar que la salida del convertidor D/C, x,(t), tiene una banda limitada a

f = 5kHz. Como Ha( f ) es un filtro de paso bajo ideal con una frecuencia de corte de 10 kHz, yo(!) =xo(t). Por lo tanto,

este sistema es equivalente al que se muestra a continuación.

Debido a que un convertidor D/C ideal seguido de un convertidor D/C ideal es el sistema de identidad, y(n) =x(n).

(b) Cuando TI + T2, este sistema, en general, ya no es un sistema lineal invariante por corrimiento. Sin embargo, podemos analizar

este sistema en el dominio de la frecuencia como sigue. Primero, tenga en cuenta que el DTFTofx(n) es como se ilustra en la siguiente

cifra:

MUESTREO [CAP. 3

Por lo tanto, la salida del convertidor D/C es una señal de banda limitada que tiene una transformada de Fourier, como se muestra en la figura.

siguiente figura:

El filtro de paso bajo analógico elimina todas las frecuencias en xa(t) por encima de 10 kHz para producir una señal y,(t) que tiene una

Transformada de Fourier como se muestra a continuación.

Debido a que la frecuencia más alta en ya(t) es de 10 kHz, la tasa de Nyquist es de 20 kHz. Sin embargo, la frecuencia de muestreo

del convertidor C/D es de 10 kHz, por lo que ya(t) tendrá un alias. La DTFT de y(n) está relacionada con Ya(jQ) de la siguiente manera:

Sumar los rendimientos transformados desplazados y escalados

Conversión de frecuencia de muestreo

3.21 Suponga que una secuencia de tiempo discreto x(n) tiene una banda limitada de modo que

Luego, esta secuencia se muestrea para formar la secuencia

donde N es un número entero. Encuentre el valor más grande de N para el cual x(n) se puede recuperar de forma única a partir de y(n).

La forma más fácil de ver este problema es como se ilustra a continuación.

Convirtiendo x(n) en una señal de tiempo continuo con un convertidor D/C ideal con una frecuencia de muestreo f, produce

una señal de tiempo continuo xa(t) que está limitada en banda a fo = 0.3. fs/2. Por lo tanto, xa(r) puede ser muestreado, sin

CAP. 31 MUESTREO

aliasing, si usamos una frecuencia de muestreo fsf 2 2fo = 0.3 f, o

Por lo tanto, si T,' = 3T,,

y(n) = x,(3nTs) =x(3n)

yx(n) puede recuperarse de forma única a partir de y(n). Por lo tanto, N = 3.

3.22 Considere el siguiente sistema:

Suponga que Xa( f) = 0 para If ( > l/Ts y que

¿Cómo se relaciona la salida del sistema de tiempo discreto, y(n), con la señal de entrada xa(t)?

En este sistema, la señal de banda limitada x,(t) se muestrea, sin solapamiento, para producir la señal muestreada x(n) =x,(nT,).

Muestreo ascendente x(n) por un factor de L, y filtrado con un filtro de paso bajo ideal con una frecuencia de corte w = n/L,

produce la señal

es decir, una señal que se muestrea con una frecuencia de muestreo L f,. Sin embargo, debido a que el filtro de paso bajo tiene fase lineal

con un retraso de grupo de una muestra, la señal muestreada interpolada se retrasa en 1. Por lo tanto, la salida del

filtro de paso bajo es

u(n) = w(n - 1) = x,

El muestreo descendente por L produce la salida

Así, y(n) corresponde a muestras de x,(c -to) donde ro = T,/L.

3.23 Considere el sistema que se muestra en la siguiente figura.

Suponga que la entrada está limitada en banda, Xa(ji2)= 0 para (i2(> 2n . 1000.

(a) ¿Qué restricciones deben imponerse a M, TI y T2 para que ya(t) sea igual a x,(t)?

(b) Si f, = f2 = 20 kHz y M = 4, encuentre una expresión para ya(r) en términos de x,(t).

S AMPLIFICACIÓN [CAP. 3

(a) Suponga que x,(r) tiene una transformada de Fourier como se muestra en la siguiente figura.

Dado que y(n) = x(Mn) = x,(nMTI), para evitar que x(n) tenga alias, es necesario que

Si se cumple esta restricción, la salida del muestreador descendente tiene una DTFT como se muestra a continuación.

Pasar por el convertidor D/C produce la señal yo([), que tiene la transformada de Fourier que se muestra a continuación.

Por lo tanto, para que yo(/) sea igual a xu(/), requerimos que

I. MTl 5 1/2000 para evitar aliasing.

2. Tz = MTI para evitar el escalado de frecuencia.

(6) Con TI = Tz = 1/20000 y M = 4, observe que

Por lo tanto, no hay aliasing. Así, como vemos en la figura anterior,

3.24 Las unidades de cinta de audio digital (DAT) tienen una frecuencia de muestreo de 48 kHz, mientras que un disco compacto (CD)

El reproductor funciona a una frecuencia de 44,1 kHz. Para grabar directamente de un CD a un DAT, es necesario

convertir la frecuencia de muestreo de 44,1 a 48 kHz. Por lo tanto, considere el siguiente sistema para realizar

esta conversión de frecuencia de muestreo:

CAP. 31 MUESTREO 135

Encuentre los valores más pequeños posibles para L y M y encuentre el filtro apropiado H(eJu) para realizar esto

conversión.

Dado que 48000 = 2'. 3 . 5' y 44100 = 22 . 32 . S2 . 72, para cambiar la tasa de muestreo que requerimos

Por lo tanto, si aumentamos la muestra en L = 160 y luego disminuimos la muestra en M = 147, logramos la frecuencia de muestreo deseada

conversión. El filtro de paso bajo que necesitamos es uno que tenga una frecuencia de corte

Tr Tr Tr

wc = min(- -) = -- L'M 160

y la ganancia del filtro debe ser igual a L = 160.

3.25 Suponga que deseamos reducir la velocidad de un segmento del habla a la mitad de su velocidad normal. La señal del habla

Se supone que sa(t) no tiene energía fuera de 5 kHz, y se muestrea a una velocidad de 10 kHz, lo que produce el

secuencia

s(n) = s,(nT,)

Se propone el siguiente sistema para crear la señal de voz ralentizada.

Suponga que Sa(jQ) es como se muestra en la siguiente figura:

(a) Encuentre el espectro de v(n).

(b) Suponga que el filtro de tiempo discreto se describe mediante la ecuación en diferencias

Encuentre la respuesta de frecuencia del filtro y describa su efecto en v(n).

(c) ¿Qué es Ya(jQ) en términos de X,(jQ)? ¿Yo(!) corresponde a un discurso lento?

(a) Dado que so(,) se muestrea a la velocidad de Nyquist, la DTFT de la señal de voz muestreada, s(n), es la siguiente:

+ WeJw)

-n TI

El muestreo ascendente por un factor de 2 escala el eje de frecuencia de S(el") por un factor de dos, como se muestra a continuación.

MUESTREO [CAP. 3

La respuesta de la muestra unitaria del filtro de tiempo discreto es

que tiene una respuesta de frecuencia

H (eJW)= I + cos w

Para ver el efecto de este filtro en v(n), tenga en cuenta que, debido al muestreo ascendente, v(n) = 0 para n impar. Por lo tanto. con

resulta que

tu (n n impar

y(n) = Iiv(n-I)+;u(n+l) niven

Por lo tanto, los valores de índice par de v(n) no cambian, y los valores de índice impar son el promedio de los dos

valores vecinos. Como resultado, h(n) realiza una interpolación lineal entre los valores de v(n).

La salida del convertidor de CC, y,,(t), tiene una transformada de Fourier

TTY(eJRTr) IS21 < TIT,

Y,(.W) =

de lo contrario

Ya que Y (ej") = H (pi''')v(ei") = ( I +cos w)~ (ej")

y v(eJw)= s(eJ2")

entonces

que es el producto de (1 +cos QT,) y T,S(~J'"~%) como se ilustra a continuación.

Así, y,(t) no corresponde al habla ralentizada debido a las imágenes de s,,(r) que se dan en la frecuencia

rango 5000n < IS21 < IOOOOn y el interpolador lineal no ideal. Tenga en cuenta que una mejor aproximación sería

usar un convertidor de CC con una frecuencia de muestreo de 2T, para eliminar las imágenes.

3.26 En la siguiente figura se muestran dos formas diferentes de conectar en cascada un muestreador ascendente con un muestreador descendente.

CAP. 31 MUESTREO

(a) Si M = L, demuestre que los dos sistemas no son idénticos.

(b) ¿Bajo qué condiciones serán idénticos los dos sistemas?

(a) En el primer sistema, que consta de un muestreador ascendente seguido de un muestreador descendente, tenga en cuenta que wl(n) es una secuencia

que se forma insertando L -I ceros entre cada valor de x(n). Luego, el muestreador extrae cada Lth

valor de wl(n), produciendo así la salida

En el segundo sistema, sin embargo, el muestreador extrae cada L-ésima muestra de s(n) y descarta el resto. El

up-sampler luego inserta L -I ceros entre cada valor de w2(nj. Por lo tanto,

Por lo tanto, los dos sistemas no son lo mismo.

(b) Para analizar estos sistemas cuando L # M, observe que yz(n) en el segundo sistema tiene la forma que se muestra en la

siguiente figura:

Por otro lado, la secuencia w,(n) en el primer sistema es como se muestra a continuación.

Tenga en cuenta que yl(n) se forma extrayendo cada valor M-ésimo de wl(n),

MUESTREO [CAP. 3

Claramente, yl(kL)= wl(kML) = x(kM)

entonces yl(kL) = yz(kL)

Sin embargo, para que yl(n) sea igual a yz(n), requerimos que

y,(n) = wl(nM) = 0 n # kL

Esto será cierto si y sólo si M y L son primos relativos.

Problemas complementarios

Conversión AID y DIA

Encuentre dos señales de tiempo continuo diferentes que producirán la secuencia

cuando se muestrea con una frecuencia de muestreo de 8 kHz.

Si la tasa de Nyquist para xu([) es R,, encuentre la tasa de Nyquist para (a) x2(2t), (b) x(t/3), (c) x(t) * x(t).

Se sabe que una señal de tiempo continuo x,(t) es recuperable de forma única a partir de sus muestrasxa(nTs) cuando T, = 1 ms. Qué

Cuál es la frecuencia más alta en Xu( f )?

Suponga que x,(t) tiene una banda limitada a 8 kHz (es decir, Xu(f) = 0 para If I 8000). (a) ¿Cuál es la tasa de Nyquist para

.%(I)? (b) ¿Cuál es la tasa de Nyquist para x,(t)cos(2n . 1000t)'?

Sea x,(t) = cos(6507ri) + 2 sen(7207rt). (a) ¿Cuál es la tasa de Nyquist para x,(t)? (b) Si xa(t) se muestrea al doble de la

Tasa de Nyquist, ¿cuáles son las frecuencias de las sinusoides en la secuencia muestreada?

Si se muestrea un filtro de tiempo continuo con una respuesta de impulso h,(r) con una frecuencia de muestreo de, ¿qué sucede?

a la frecuencia de corte w,. del filtro de tiempo discreto a medida que 1, se incrementa?

Una señal de paso de banda compleja x,(r) con Xu(f') distinta de cero para 10 kHz < f < 12 kHz se muestrea a una frecuencia de muestreo de

2 kHz. La secuencia resultante es

¿Qué es x,(t)?

Si la frecuencia más alta en x,(t) es f = 8 kHz, encuentre la frecuencia de muestreo mínima para la señal de paso de banda

y,(t) = x,(OCOS(R~I)si (a) Ro = 27r . 20 . 10' y (b) Ro = 217 . 24 . lo3.

La señal de tiempo continuo x,(t) = 7,25 cos(20007rt) se muestrea a una frecuencia de muestreo de 8 kHz y se cuantifica

con una resolución A = 0.02. ¿Cuántos bits se requieren en el convertidor AID para evitar el recorte de xu([)?

Suponga que queremos muestrear la señal x,(t) con un cuantificador de 12 bits, donde se supone que x,(t) es gaussiana con

una varianza u,?. ¿Cuál es la relación señal-ruido de cuantificación si queremos que el rango del cuantificador se extienda desde

-30, a 3ax?

Suponga que se muestrea una forma de onda analógica con una frecuencia de muestreo de 10 kHz y que xu([) contiene un

fuerte señal de interferencia de 60 Hz. Si la única información en x,(r) de interés está en la banda de frecuencia anterior

CAP. 31 MUESTREO

60 Hz, la interferencia se puede eliminar con un filtro de paso alto de tiempo discreto que tiene una respuesta de frecuencia de

la forma

¿Cuál es la frecuencia de corte más pequeña w, que se puede usar y aun así eliminar la interferencia de 60 Hz?

3.38 Verdadero o falso: si x(n) tiene una transformada de Fourier de tiempo discreto que es igual a cero para n/4 < Iwl I r,

Procesamiento en tiempo discreto de señales analógicas

El sistema que se muestra en la figura 3-9 puede usarse para procesar una señal analógica con un sistema de tiempo discreto. Asumir que

x,(t) tiene una banda limitada con X,(f) = 0 para If 1 > 10 kHz, como se muestra en la siguiente figura.

Si el sistema de tiempo discreto es un filtro de paso bajo ideal con una frecuencia de corte de n/4, encuentre la transformada de Fourier de

yo([)cuando (a) fi = 20 kHz y f2 = 10 kHz y (b)fl = 10 kHz y fi = 20 kHz.

Para señales de entrada de banda limitada, el sistema que se muestra en la figura 3-10 es un sistema de tiempo continuo lineal e invariante en el tiempo.

Si

Encuentre la respuesta de frecuencia del sistema de tiempo continuo equivalente.

Para señales de entrada de banda limitada, el sistema que se muestra en la figura 3-10 es un sistema de tiempo continuo lineal e invariable en el tiempo. Si

el sistema general debe ser un diferenciador,

¿Cómo debe definirse la respuesta de frecuencia del sistema de tiempo discreto?

Conversión de frecuencia de muestreo

3.42 El muestreador ascendente y el muestreador descendente son componentes que se encuentran en interpoladores y diezmadores, respectivamente. Son

estos sistemas lineales? ¿Son invariantes al cambio?

3.43 Una secuencia x(n) corresponde a muestras de una señal de banda limitada utilizando una frecuencia de muestreo de 10 kHz. Sin embargo,

la secuencia debería haber sido muestreada usando una frecuencia de muestreo f, = 12 kHz. Diseñar un sistema para digitalmente

cambiar la frecuencia de muestreo.

3.44 Una señal x,(r) con banda limitada a 10 kHz es procesada por el siguiente sistema:

MUESTREO [CAP. 3

10 de lo contrario

exprese la salida ya(t) en términos de la entrada xa(t).

Respuestas a problemas complementarios

xl(t)= cos(12rn~t) yx2(t)= cos(172~nt).

(a)4R,. (b)R,/3.(c) R,.

500 Hz.

(a) 16kHz. (b) 18kHz.

o, disminuye.

(a) 56kHz. (b) 32kHz.

10 bits

73,51 dB.

o,= 0.012n.

Verdadero.

CAP. 31 MUESTREO

1 hora

1Ql -= - 3.40 Ha(jR) = TY

de lo contrario

3.41 H (el") = jw/T, para lo1 < n.

3.42 Ambos son lineales y variables por turnos.

3.43 Muestreo ascendente por L = 6, filtro con un filtro de paso bajo que tiene una frecuencia de corte de 0,. = ~/6 y una ganancia de 6, y

reducir la muestra por M = 5.

Capítulo 4. La transformación Z 

 

4.1 Introducción 

 

4.2 Definición de la transformada z 

 

4.3 Propiedades 

4.4 La transformada z inversa 

 

4.4.1 Expansión de fracciones parciales 

 

4.4.2 Serie de potencia 

 

4.4.3 Integración de contornos 

 

4.5 La transformada z unilateral 

 

Problemas Resueltos 

 

Capítulo 5. Análisis transformado de sistemas 

 

5.1 Introducción 

 

5.2 Función del sistema 

 

5.2.1 Estabilidad y causalidad 

 

5.2.2 Sistemas inversos 

 

5.2.3 Respuesta de muestra unitaria para funciones de sistemas racionales 

 

5.2.4 Respuesta de frecuencia para funciones de sistemas racionales 

 

5.3 Sistemas con fase lineal 

 

5.4 Filtros paso total 

 

5.5 Sistemas de fase mínima 

 

5.6 Sistemas de retroalimentación 

 

Problemas Resueltos 

 

Capítulo 6. El DFT 

 

6.1 Introducción 

 

6.2 Serie discreta de Fourier 

 

6.3 Transformada de Fourier discreta 

 

6.4 Propiedades DFT 

 

6.5 Muestreo del DTFT 

 

6.6 Convolución lineal usando el DFT 

 

Problemas Resueltos 

 

Capítulo 7. La transformada rápida de Fourier 

 

7.1 Introducción 

 

7.2 Algoritmos Radix-2 FFT 

 

7.2.1 Decimación en el tiempo FFT 

 

7.2.2 FFT de diezmado en frecuencia 

 

7.3 Algoritmos FFT para compuesto N 

 

7.4 Factor primo FFT 

 

Problemas Resueltos 

 

Capítulo 8. Implementación de sistemas de tiempo discreto 

 

8.1 Introducción 

 

8.2 Redes digitales 

 

8.3 Estructuras para sistemas FIR 

 

8.3.1 Formulario Directo 

 

8.3.2 Cascada Formulario 

 

8.3.3 Filtros de fase lineal 

 

8.3.4 Muestreo de frecuencia 

 

8.4 Estructuras para sistemas IIR 

 

8.4.1 Formulario Directo 

 

8.4.2 Cascada Forma 

 

8.4.3 Estructura paralela 

 

8.4.4 Estructuras transpuestas 

 

8.4.5 Filtros paso total 

 

8.5 Filtros de celosía

 

8.5.1 Filtros de celosía FIR 

 

8.5.2 Filtros de red de todos los polos 

 

 

8.5.3 Filtros de celosía IIR 

 

8.6 Efectos de longitud de palabra finita 

 

8.6.1 Representación binaria de números 

 

8.6.2 Cuantización de coeficientes de filtro 

 

8.6.3 Ruido de redondeo 

 

8.6.4 Emparejamiento y pedidos 

 

8.6.5 Desbordamiento 

 

Problemas Resueltos 

 

Capítulo 9. Diseño de filtros 

 

9.1 Introducción 

 

9.2 Especificaciones del filtro 

 

9.3 Diseño de filtro FIR 

 

9.3.1 Diseño FIR de fase lineal con Windows 

 

9.3.2 Diseño de filtro de muestreo de frecuencia 

 

9.3.3 Filtros de fase lineal Equiripple 

 

9.4 Diseño de filtro IIR 

 

9.4.1 Prototipos de filtro de paso bajo analógico 

 

9.4.2 Diseño de filtros IIR a partir de filtros analógicos 

 

9.4.3 Transformaciones de frecuencia 

 

9.5 Diseño de filtros basado en un enfoque de mínimos cuadrados 

 

9.5.1 Aproximación de pad 

 

9.5.2 Método de Prony 

 

9.5.3 Inversa de mínimos cuadrados FIR 

 

Problemas Resueltos